Chapter 1 8 The Number Of Roots Of A Quadratic Equation Pdf To determine the number of real solutions for each quadratic equation, we can use the discriminant method. the discriminant is part of the quadratic formula: ± b 4 and it is represented by the expression inside the square root, b2 − 4ac. Answer for 52: the discriminant is 144, there are 2 distinct real roots (4 and 8).
Solved Find The Number Of Real Roots Of Each Quadratic Chegg To solve for x in x 2 x 3 = 0, substitute a = 1, b = 1, and c = 3 into the quadratic formula. this tool eliminates the need for guessing and provides an algebraic method to solve quadratic equations, no matter how complex they appear. The symbolab quadratic equation calculator helps you solve quadratic equations step by step. whether you're practicing, checking your homework, or learning how the process works, this tool gives clear explanations at every stage. Discriminant = b^2 4ac. if the discriminant is positive, there are two real roots. the parabola crosses the x axis, then crosses back. if the discriminant is zero, there is one real root. the parabola touches the x axis but does not cross it. if the discriminant is negative, there are no real roots. the parabola never touches the x axis. For the equation $$x^ {2} 7x 10=0$$x2 7x 10= 0, calculate the discriminant: $$\triangle = b^ {2} 4ac = 7^ {2} 4 (1) (10) = 49 40 = 9$$ = b2 −4ac = 72−4(1)(10) = 49−40 =9. since $$\triangle > 0$$ > 0, there are two real solutions.
Solved Find The Roots Of The Given Quadratic Equation Chegg Discriminant = b^2 4ac. if the discriminant is positive, there are two real roots. the parabola crosses the x axis, then crosses back. if the discriminant is zero, there is one real root. the parabola touches the x axis but does not cross it. if the discriminant is negative, there are no real roots. the parabola never touches the x axis. For the equation $$x^ {2} 7x 10=0$$x2 7x 10= 0, calculate the discriminant: $$\triangle = b^ {2} 4ac = 7^ {2} 4 (1) (10) = 49 40 = 9$$ = b2 −4ac = 72−4(1)(10) = 49−40 =9. since $$\triangle > 0$$ > 0, there are two real solutions. Solve your quadratic equations step by step! solves by factoring, square root, quadratic formula methods.
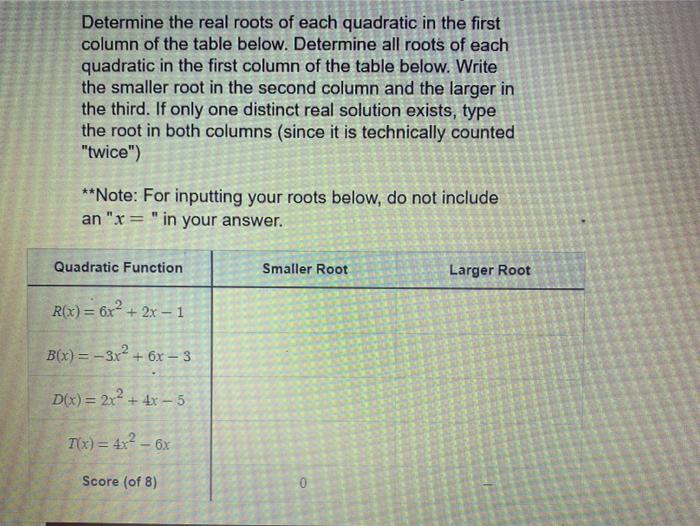
Solved Determine The Real Roots Of Each Quadratic In The Chegg Solve your quadratic equations step by step! solves by factoring, square root, quadratic formula methods.
Solved Without Solving Determine The Number Of Real Roots Chegg
Comments are closed.