Solved For Every N%d0%b2 N Show That %d0%b2 J 1nj 2n N 1 And Chegg

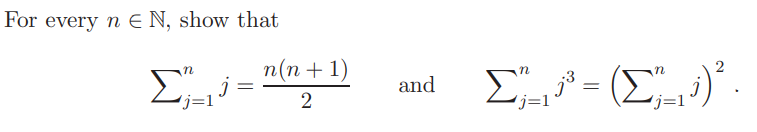
Solved For Every Nв N Show That в J 1nj 2n N 1 And Chegg Let d0, d1, d2, . . . be defined by the formula dn = 3n − 2n for all integers n ≥ 0. show that this sequence satisfies the recurrence relation: dk = 5 dk−1 − 6 dk−2. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Let d 0, d 1, d 2, be defined by the formula d n = 3 n 2 n for all integers n ≥ 0. show that this sequence satisfies the recurrence relation. d k = 5d k 1 6d k 2.

Solved A Show That For Every Nв N We Have 2n N B Deduce Chegg The student is dealing with a mathematical sequence defined by a given formula and is tasked to show that the sequence satisfies a particular recurrence relation. Join today and access millions of expert created videos, each one skillfully crafted to teach you how to solve tough problems step by step. Let d 0 , d 1 , d 2 , be defined by the formula d n = 3 n − 2 n for every integer n ≥ 0 . show that this sequence satisfies the following recurrence d k = 5 d k − 1 − 6 d k − 2. The sequence is defined recursively by d = 1, d1 = 16, and dn = 3dn 1 10dn 2 for n > 2. use the characteristic equation of the recurrence relation to find the explicit formula for this sequence.

Solved Exercise 5 Show That For Every Nв N We Have Chegg Let d 0 , d 1 , d 2 , be defined by the formula d n = 3 n − 2 n for every integer n ≥ 0 . show that this sequence satisfies the following recurrence d k = 5 d k − 1 − 6 d k − 2. The sequence is defined recursively by d = 1, d1 = 16, and dn = 3dn 1 10dn 2 for n > 2. use the characteristic equation of the recurrence relation to find the explicit formula for this sequence. Given a set of $n 1$ numbers out of the first $2n$ natural numbers, $\ {1,2,\ldots,2n\}$, prove that there are two numbers in the set, one of which divides the other. The last expression is obviously equal to the right hand side of (16). this proves the inductive step. therefore, by the principle of mathematical induction, the given statement is true for every positive integer n. Step 1: substitute the given formula for dn into the recurrence relation dk = dk 1 6dk 2. show more…. Question: let d0, d1, d2, … be a sequence defined by the formula dn = 3n − 2n for every integer n ≥ 0. fill in the blanks to show that d0, d1, d2, … satisfies the following recurrence relation. dk = 5dk − 1 − 6dk − 2 for every integer k ≥ 2.