
Solved Hw Section 5 5 Alternating Series Problem 5 The Chegg Hw section 5.5 alternating series: problem 5 the alternating series test. we want to check for convergence of the series ∑ n = 1 ∞ ( − 1 ) n 1 2 n n and we have decided to try the alternating series test. About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket press copyright.

Solved Hw Section 5 5 Alternating Series Problem 16 Chegg Now, with expert verified solutions from calculus, volume 2 1st edition, you’ll learn how to solve your toughest homework problems. our resource for calculus, volume 2 includes answers to chapter exercises, as well as detailed information to walk you through the process step by step. This video contains solutions to sample problems from openstax calculus, volume 2, section 5.5: alternating series. openstax calculus vol. 2: opensta. An alternating series is a series whose terms consistently alternate in sign. every alternating series can be written in the form where . (notice how we are separating the sign from . we haven't done that before.) examples 1 here are some alternating series a. b. c. here are some series that are not alternating series d. e. Alternating series is conditionally convergent. 1. determine the convergence of the following alternating series using alternating series test. (ast). 2. test the given series for absolute convergence, conditional convergence, or divergence.

Solved Hw Section 5 5 Alternating Series Problem 11 Chegg An alternating series is a series whose terms consistently alternate in sign. every alternating series can be written in the form where . (notice how we are separating the sign from . we haven't done that before.) examples 1 here are some alternating series a. b. c. here are some series that are not alternating series d. e. Alternating series is conditionally convergent. 1. determine the convergence of the following alternating series using alternating series test. (ast). 2. test the given series for absolute convergence, conditional convergence, or divergence. Hw section 5.5 alternating series: problem 1 the alternating series test. we want to check for convergence of the series ∑n=1∞(−1)n 1n1 (the alternating harmonic series) and we have decided to try the alternating series test. Paste the direct link of the chegg or course hero question into the search box. you can also type your question into homeworkify’s q&a search engine for similar solutions. hit ‘search’ to get your answers. Hw section 5.5 alternating series dr. vu nguyen ( references: webwork calculus ii utsa; openstax volume ii) theorem ( the alternating series test) an alternating series is a series that can be written in the form ∞ ∑ n=1 (−1)n 1 bn= b1−b2 b3 − this series converges if all three of the following conditions are satisfied: 1. 1. find the radius and interval of convergence for the series n=1 xn n. solution. using the ratio test, we have = lim n xn 1 n 1 xn n = x. the series converges when |x| < 1 and diverges when |x| > 1, so the radius of convergence is 1. if x = 1, the series is n=1 1 n, and it diverges by the p series test (as p < 1). if x = 1, the series is n=1.
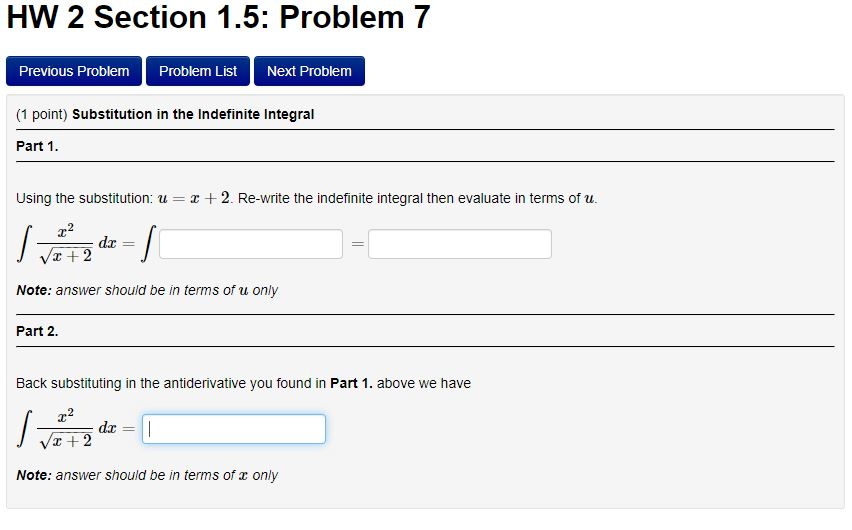
Solved Hw 2 Section 1 5 Problem 7 Previous Problem Problem Chegg Hw section 5.5 alternating series: problem 1 the alternating series test. we want to check for convergence of the series ∑n=1∞(−1)n 1n1 (the alternating harmonic series) and we have decided to try the alternating series test. Paste the direct link of the chegg or course hero question into the search box. you can also type your question into homeworkify’s q&a search engine for similar solutions. hit ‘search’ to get your answers. Hw section 5.5 alternating series dr. vu nguyen ( references: webwork calculus ii utsa; openstax volume ii) theorem ( the alternating series test) an alternating series is a series that can be written in the form ∞ ∑ n=1 (−1)n 1 bn= b1−b2 b3 − this series converges if all three of the following conditions are satisfied: 1. 1. find the radius and interval of convergence for the series n=1 xn n. solution. using the ratio test, we have = lim n xn 1 n 1 xn n = x. the series converges when |x| < 1 and diverges when |x| > 1, so the radius of convergence is 1. if x = 1, the series is n=1 1 n, and it diverges by the p series test (as p < 1). if x = 1, the series is n=1.
