
Doc 20 D1 81 D2 B1 D1 80 D0 B0 D2 9b 20 D0 B6 D0 B0 D1 83 D0 B0 D0 There are 2 steps to solve this one. to find a vector b such that comp a b = 2, use the formula comp a b = a ⋅ b | a |, and write b as b 1, b 2, b 3 null . if a = (3, 0, 1), find a vector b such that comp a b = 2. not the question you’re looking for? post any question and get expert help quickly. If a = (3, 0, 1), find a vector b such that comp a b = 2.
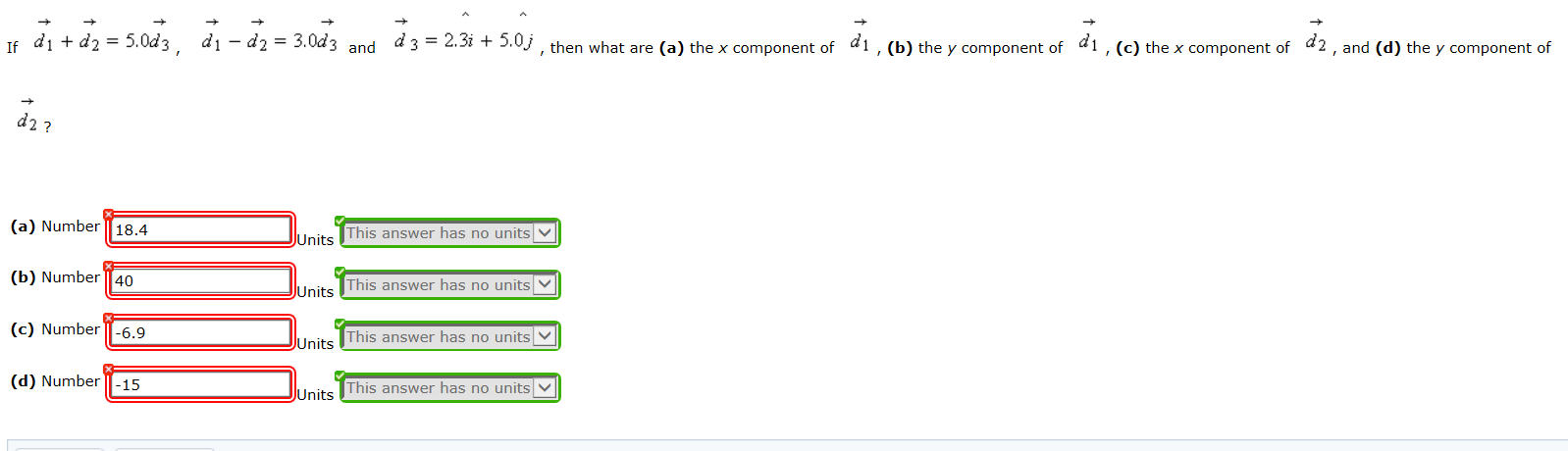
Solved If D1 D2 5 0d3 D1 D2 3 0d3 And D3 2 3i Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. we need to find a vector b → such that c o m p a b = 4 . not the question you’re looking for? post any question and get expert help quickly. If a = 3, 0, −1 , find a vector b such that compab = 2. the correct vector b that satisfies the condition compab=2, given vector a <3, 0, 1>, is option c <6, 0, 2>. the procedure involves calculating the dot product of vector b with vector a and ensuring it equals twice the magnitude of vector a. We are given a vector a = 3, 0, − 1 and we need to find another vector b such that the component of b in the direction of a is a certain value (usually given in fulsome problems, but we aren't provided a specific value here, which suggests we might be looking at the vector form). Step 1: formula and concept used for finding vector b . the expression for scalar projection of b onto a is: compab= f racacdotb∣a∣ (1) consider a general expression to find the dot product between two three dimensional vectors. a cdotb= lef t langlea1,a2,a3 right rangle cdot lef t langleb1,b2,b3 right ranglea cdotb=a1b1 a2b2 a3b3.
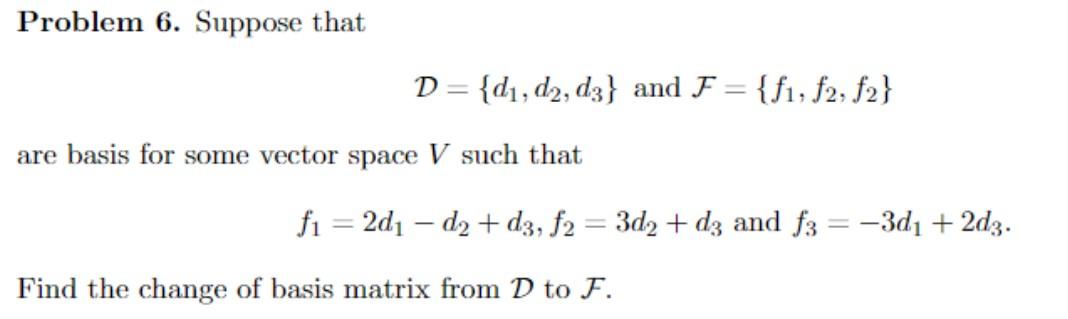
Solved Problem 6 Suppose That D D1 D2 D3 And F F1 F2 F2 Chegg We are given a vector a = 3, 0, − 1 and we need to find another vector b such that the component of b in the direction of a is a certain value (usually given in fulsome problems, but we aren't provided a specific value here, which suggests we might be looking at the vector form). Step 1: formula and concept used for finding vector b . the expression for scalar projection of b onto a is: compab= f racacdotb∣a∣ (1) consider a general expression to find the dot product between two three dimensional vectors. a cdotb= lef t langlea1,a2,a3 right rangle cdot lef t langleb1,b2,b3 right ranglea cdotb=a1b1 a2b2 a3b3. We are given a = [3, 0, − 1] \textbf{a}=[3,0, 1] a = [3, 0, − 1] and comp a b = 2 \text{comp} {\textbf{a}}\textbf{b}=2 comp a b = 2. using this formula, we can solve for a general formula for b \textbf{b} b (the vector is not unique). Use the fact that \text {comp} {\mathbf {a}}\mathbf {b}=2 compab= 2 to set up an equation, then solve the equation for b 3 b3. \begin {aligned} \frac {3b 1 b 3} {\sqrt {10}}&= 2 \\3b 1 b 3 &=2\sqrt {10}\\b 3 &=3b 1 2\sqrt {10}\end {aligned} 103b1 −b3 3b1 −b3 b3 = 2 = 2 10 = 3b1 −2 10. This problem has been solved: solutions for chapter 13.3 problem 43e: if a = 3, 0, −1 , find a vector b such that compa b = 2. … get solutions get solutions get solutions done loading looking for the textbook?. Q: let à = ( 5, 2, 4) and b = ( 1,5, 3). find a x b. (enter your answer as a vector of the form .)….

Productivity D1 D2 D3 D1 D2 D3âž âž 1231 2131 31 31âž âž Chegg We are given a = [3, 0, − 1] \textbf{a}=[3,0, 1] a = [3, 0, − 1] and comp a b = 2 \text{comp} {\textbf{a}}\textbf{b}=2 comp a b = 2. using this formula, we can solve for a general formula for b \textbf{b} b (the vector is not unique). Use the fact that \text {comp} {\mathbf {a}}\mathbf {b}=2 compab= 2 to set up an equation, then solve the equation for b 3 b3. \begin {aligned} \frac {3b 1 b 3} {\sqrt {10}}&= 2 \\3b 1 b 3 &=2\sqrt {10}\\b 3 &=3b 1 2\sqrt {10}\end {aligned} 103b1 −b3 3b1 −b3 b3 = 2 = 2 10 = 3b1 −2 10. This problem has been solved: solutions for chapter 13.3 problem 43e: if a = 3, 0, −1 , find a vector b such that compa b = 2. … get solutions get solutions get solutions done loading looking for the textbook?. Q: let à = ( 5, 2, 4) and b = ( 1,5, 3). find a x b. (enter your answer as a vector of the form .)….
