
Solved If A Bв Z Then A2в 4b 2 Which Method Of Proof Would Chegg If a, b ∈ z, then a 2 − 4 b = 2. which method of proof would be the best and most suitable appropriate to prove the statement above? (a) contrapositive implication (b) contradiction (c) direct proof (d) induction suppere x ∈ z. if i x 9 is enen, then x soold which. My solution : we suppose that is true. then by contradiction: $a^2 4b 2=0$ $a^2=4b 2$ $a=2(b 1 2) ^{0.5}$ then $(b 1 2)$ is fraction and rooted by $0.5$ so the square root of any fraction $ $ any.
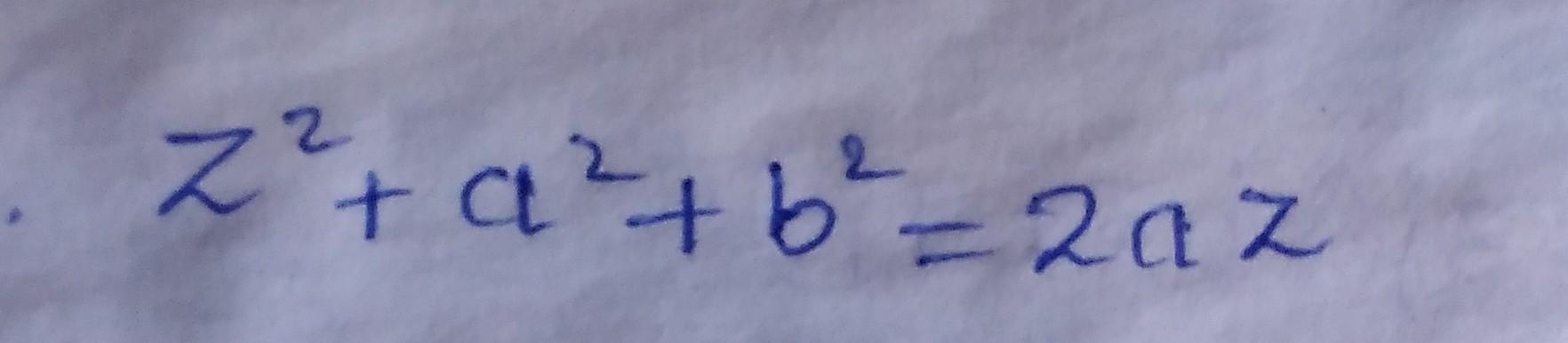
Solved Z2 A2 B2 2az Chegg If a,b ∈ z then a2−4b ≠ 2. as, any irrational multiplied by other irrational number gives a irrational number. but, a is given to be integer. which contradicts that a2−4b = 2. thus, if a,b ∈ z then a2−4b ≠ 2. is this answer helpful? hence we get a = irrational number which contradicts that it is an integer. Prove that if a, b ∈ z, then a2 − 4b − 2 = 0. to prove that a2 − 4b − 2 = 0 for any integers a and b, we can analyze the possible values of both sides of the equation. step 1: express the equation in a suitable form. assume, for contradiction, that there exist integers a and b such that: a2 − 4b − 2 = 0. this can be rewritten as: a2 = 4b 2. There are 2 steps to solve this one. step 1: assume not the question you’re looking for? post any question and get expert help quickly. answer to if a, b z then a^2 4b 2 ≠ 0. solve by. Use a proof by contradiction to show if a, b ∈ z, then a 2 − 4 b − 2 = 0. (hint: use a result from class which states if a 2 is odd then a is also odd.) prove that if a and b are odd integers, then 4 ∤ (a 2 b 2).

Solved 5 Solve Each Equation For Z A Bi A 2z I 2 9i B Chegg There are 2 steps to solve this one. step 1: assume not the question you’re looking for? post any question and get expert help quickly. answer to if a, b z then a^2 4b 2 ≠ 0. solve by. Use a proof by contradiction to show if a, b ∈ z, then a 2 − 4 b − 2 = 0. (hint: use a result from class which states if a 2 is odd then a is also odd.) prove that if a and b are odd integers, then 4 ∤ (a 2 b 2). Exercises for chapter 10 a. use the method of proof by contradiction to prove the following statements. (in each case, you should also think about how a direct or contrapositive proof would work. you will find in most cases that proof by contradiction is easier.) 1. suppose n ∈z. if n is odd, then n2 is odd. 2. suppose n ∈z. Solve for $$a^ {2}$$a2, which gives $$a^ {2}=4b 3$$a2 = 4b 3. since $$a∈z$$a ∈ z, $$a^ {2}$$a2 must be an even number. since $$4b$$4b is an integer (because $$b∈z$$b ∈ z), $$4b$$4b must be either even or odd. however, if $$4b$$4b is even, then $$4b 3$$4b 3 is odd, and if $$4b$$4b is odd, then $$4b 3$$4b 3 is even. There’s just one step to solve this. let's suppose that given statement is true. then by contradiction: (b) show that if a,b∈z then a2−4b =2 using proof by contradiction. not the question you’re looking for? post any question and get expert help quickly. Solution for use the method of proof by contradiction to prove the following statement. suppose a,b z. if 4 (a2 b2), then a and b are not both odd.

Solved If Z 2 5 ï And B 25 ï Then Chegg Exercises for chapter 10 a. use the method of proof by contradiction to prove the following statements. (in each case, you should also think about how a direct or contrapositive proof would work. you will find in most cases that proof by contradiction is easier.) 1. suppose n ∈z. if n is odd, then n2 is odd. 2. suppose n ∈z. Solve for $$a^ {2}$$a2, which gives $$a^ {2}=4b 3$$a2 = 4b 3. since $$a∈z$$a ∈ z, $$a^ {2}$$a2 must be an even number. since $$4b$$4b is an integer (because $$b∈z$$b ∈ z), $$4b$$4b must be either even or odd. however, if $$4b$$4b is even, then $$4b 3$$4b 3 is odd, and if $$4b$$4b is odd, then $$4b 3$$4b 3 is even. There’s just one step to solve this. let's suppose that given statement is true. then by contradiction: (b) show that if a,b∈z then a2−4b =2 using proof by contradiction. not the question you’re looking for? post any question and get expert help quickly. Solution for use the method of proof by contradiction to prove the following statement. suppose a,b z. if 4 (a2 b2), then a and b are not both odd.
