Solved If B 1 0 1 2 1 2 2 1 2 Then Det B5 Chegg
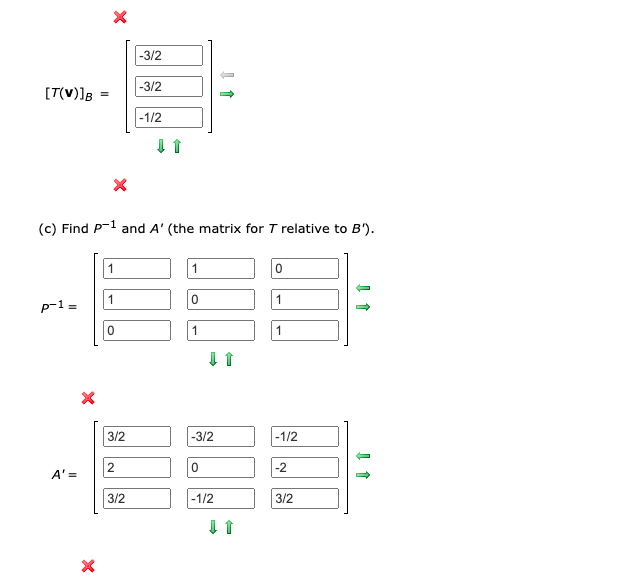
Solved Let B 0 1 1 1 1 0 1 0 1 And B Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. Applying theorem for determinants to triangular matrices we get det$ (b) = 1*1* ( 4)= 4$.

Solved Let B 0 1 1 1 0 1 1 1 0 And B Chegg Since the determinant of a product of matrices is the product of their determinants, we have: det (b^5) = (det (b))^5 now, we know that det (b) = 1, so: det (b^5) = ( 1)^5. We have, a= [ (1, 2, 1), ( 1, 1, 2), ( 2, 1, 1)] ∣a∣=1 (1 2)−2 (−1−4)−1 (1−2) =3 10 1=14 we know that, for a square matrix of order n, adj (adja)=∣a∣^ (n−2)a, if ∣a∣!=0 det (adj (adja))=∣∣a∣^ (n−2)a∣ det (adj (adja))= ( (∣a∣^ (n−2)))^n∣a∣ det (adj (adja))=∣a∣^ (n^2−2n 1) here, n=3 and ∣a∣=14. Wolfram|alpha is the perfect resource to use for computing determinants of matrices. it can also calculate matrix products, rank, nullity, row reduction, diagonalization, eigenvalues, eigenvectors and much more. use plain english or common mathematical syntax to enter your queries. For an invertible matrix a, adj (a) = det (a) * a⁻¹. the determinant of the adjugate is related to the determinant of the original matrix. we are given the matrix a = 1 1 0 2 0 1 α 1 2 and the condition det(adj(2a−at)⋅ adj(a−2at)) = 28. we need to find (det(a))2. at = 1 2 α 1 0 1 0 1 2.
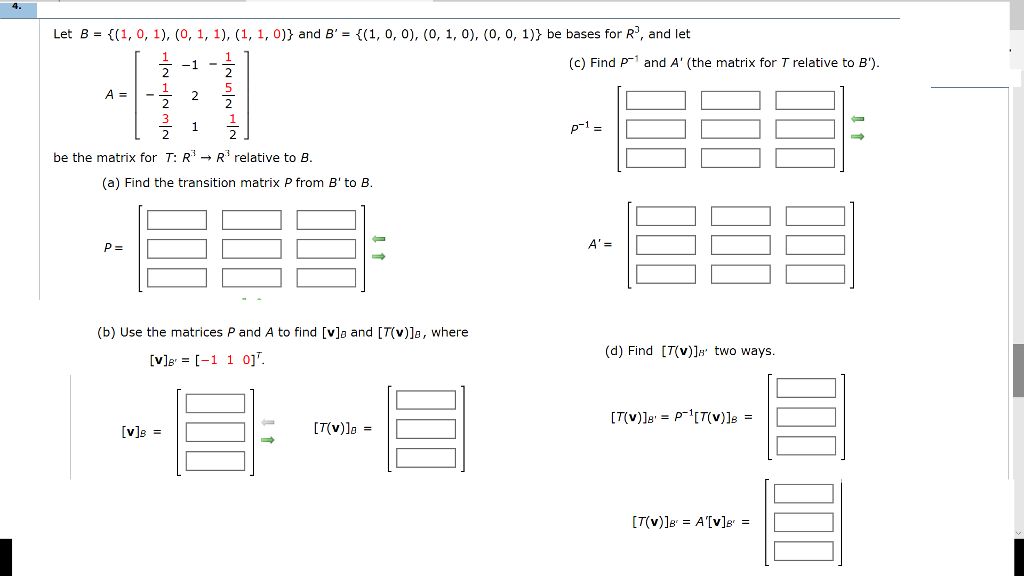
Solved Let B 1 0 1 0 1 1 1 1 0 And B Chegg Wolfram|alpha is the perfect resource to use for computing determinants of matrices. it can also calculate matrix products, rank, nullity, row reduction, diagonalization, eigenvalues, eigenvectors and much more. use plain english or common mathematical syntax to enter your queries. For an invertible matrix a, adj (a) = det (a) * a⁻¹. the determinant of the adjugate is related to the determinant of the original matrix. we are given the matrix a = 1 1 0 2 0 1 α 1 2 and the condition det(adj(2a−at)⋅ adj(a−2at)) = 28. we need to find (det(a))2. at = 1 2 α 1 0 1 0 1 2. We have that $ ( 5, 7, 9) = 3 (1, 1, 1) 2 (1, 2, 3)$ and so our determinant is $ 3\cdot ( 2) 2\cdot ( 1) = 8$. you must log in to answer this question. find the answer to your question by asking. see similar questions with these tags. Question answered step by step compute det b^4, where b= [ 1 0 1 1 1 2 1 2 1 ]. Step by step video & image solution for if a= [ (1,2, 1), ( 1,1,2), (2, 1,1)], then det (adj (adja)) is by maths experts to help you in doubts & scoring excellent marks in class 12 exams. Introduction to linear algebra: strang) if the en tries in every row of a square matrix a add to zero, solve ax = 0 to prove that det a = 0. if those entries add to one, show that det(a − i) = 0.
Comments are closed.