Solved If Det A B C 1 1 1 D E F 3 And Det A B Chegg

Solved Show That Det 1 1 1 1 A B C D A 2 B 2 C 2 D 2 Chegg If det ( a, b, c, 1, 1, 1, d, e, f) = 3 and det (a, b, c, 1, 2, 3, d, e, f)= 1, then det (a, b, c, 1, 3, 5, d, e, f)= ??? your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Note that the determinant is a multilinear function (or if you prefer in this case a $3$ tensor). we have that $ ( 5, 7, 9) = 3 (1, 1, 1) 2 (1, 2, 3)$ and so our determinant is $ 3\cdot ( 2) 2\cdot ( 1) = 8$.

Solved If Det A B C 1 1 1 D E F 4 And Det A B C 1 2 Chegg We want to find the determinant of matrix c: c = a −4 d b −6 e c −8 f. we can use the **properties **of determinants to find det (c) by subtracting a multiple of the second row of b from the third row of a to get c: c = a − 3b. now, let's compute det (c): det(c) = det(a − 3b). These are easily verified directly: write a = a b d , b = ( r s ), etc. the third property benefits from a little expansion: writing a matrix in terms of its columns, determinant can be thought of as a function. Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. So first we need to verify that the determinant of eight times b is equal to the determinant of b times a. and in the same way we need to check if the determinant of the some of the matrices is equal to the sum of the determinants.

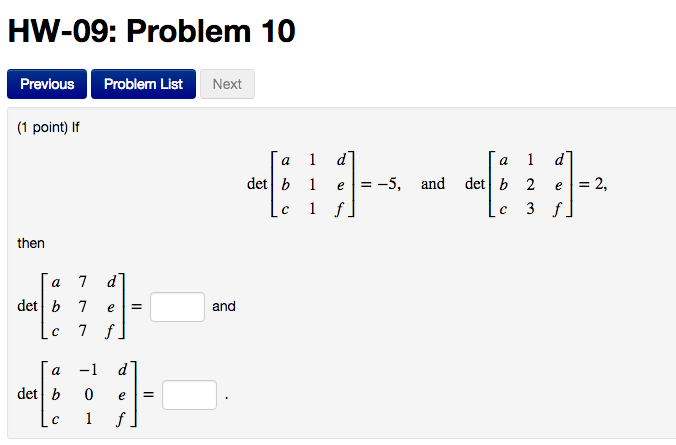
Solved If Det A B C 1 1 1 D E F 5 And Det A Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. So first we need to verify that the determinant of eight times b is equal to the determinant of b times a. and in the same way we need to check if the determinant of the some of the matrices is equal to the sum of the determinants. Final answer: in the context of mathematics, the value of det⎡⎣⎢abc222def⎤⎦⎥ is determined to be 10 based on the proportional rules of determinants in the matrices. explanation: in mathematics, the problem presented is concerned with inversely proportional matrices. To start solving the problem, first recognize the procedure when one column of a determinant is multiplied by a scalar, such as the factor of 7 multiplying the second column in the given determinant . let's denot if det [a b c 1 1 1 d e f] = 5 and det [a b c 1 2 3 d e f] = 2, then det [a b c 7 7 7 d e f] = and det [a b c 1 0 1 d e f] = . Therefore: det ( a 1 d, b 3 e b 1 e, c 2 f) 1 = 4 solving for det ( a 1 d, b 3 e b 1 e, c 2 f), we get: det ( a 1 d, b 3 e b 1 e, c 2 f) = 5 now we can use the same operations to find the determinants of the other matrices: det ( a 3 d, b 3 e, c 3 f) = det ( a 1 d, b 3 e, c 2 f) = ( 1) * 4 = 4 det ( a 3 d, b 5 e, c 7 f) = det. To find the values of the determinants, we will calculate them step by step using the properties of 3x3 matrices. this expression is quite complex, but it can be organized for clarity. thus, the two final results are: det a b c 1 1 1 d e f = aef − bde.

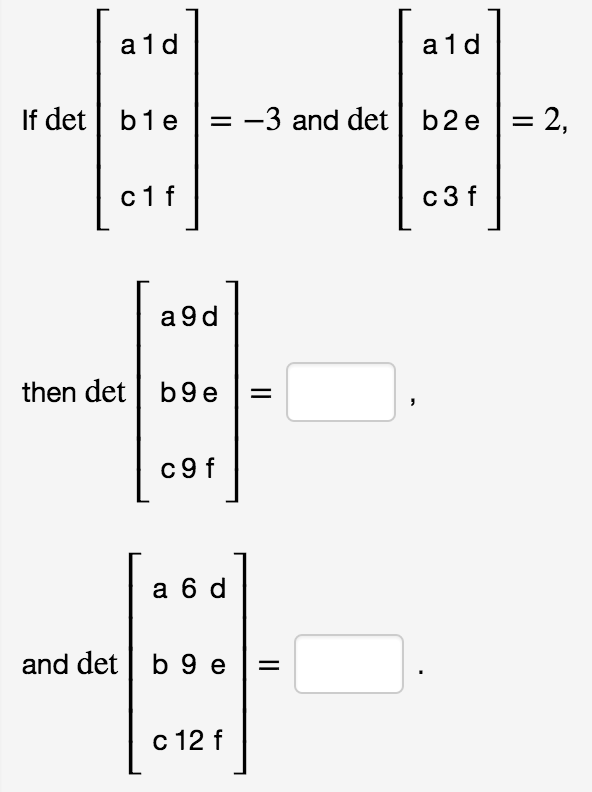
Solved If Det A 1 D B 1 E C 1 F 3 And Det A 1 D B 2 Chegg Final answer: in the context of mathematics, the value of det⎡⎣⎢abc222def⎤⎦⎥ is determined to be 10 based on the proportional rules of determinants in the matrices. explanation: in mathematics, the problem presented is concerned with inversely proportional matrices. To start solving the problem, first recognize the procedure when one column of a determinant is multiplied by a scalar, such as the factor of 7 multiplying the second column in the given determinant . let's denot if det [a b c 1 1 1 d e f] = 5 and det [a b c 1 2 3 d e f] = 2, then det [a b c 7 7 7 d e f] = and det [a b c 1 0 1 d e f] = . Therefore: det ( a 1 d, b 3 e b 1 e, c 2 f) 1 = 4 solving for det ( a 1 d, b 3 e b 1 e, c 2 f), we get: det ( a 1 d, b 3 e b 1 e, c 2 f) = 5 now we can use the same operations to find the determinants of the other matrices: det ( a 3 d, b 3 e, c 3 f) = det ( a 1 d, b 3 e, c 2 f) = ( 1) * 4 = 4 det ( a 3 d, b 5 e, c 7 f) = det. To find the values of the determinants, we will calculate them step by step using the properties of 3x3 matrices. this expression is quite complex, but it can be organized for clarity. thus, the two final results are: det a b c 1 1 1 d e f = aef − bde.

Solved It Det A B C 1 1 1 D E F 4 And Det A B Chegg Therefore: det ( a 1 d, b 3 e b 1 e, c 2 f) 1 = 4 solving for det ( a 1 d, b 3 e b 1 e, c 2 f), we get: det ( a 1 d, b 3 e b 1 e, c 2 f) = 5 now we can use the same operations to find the determinants of the other matrices: det ( a 3 d, b 3 e, c 3 f) = det ( a 1 d, b 3 e, c 2 f) = ( 1) * 4 = 4 det ( a 3 d, b 5 e, c 7 f) = det. To find the values of the determinants, we will calculate them step by step using the properties of 3x3 matrices. this expression is quite complex, but it can be organized for clarity. thus, the two final results are: det a b c 1 1 1 d e f = aef − bde.

Solved If Det A B C 1 1 1 D E F 3 And Det A B Chegg