
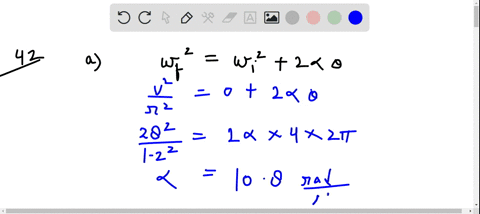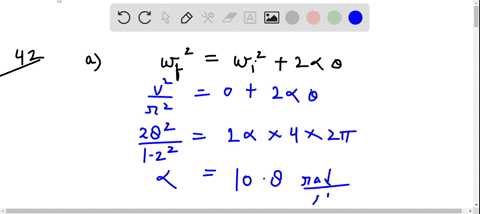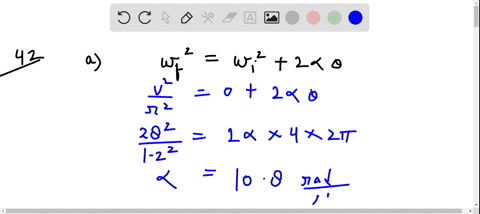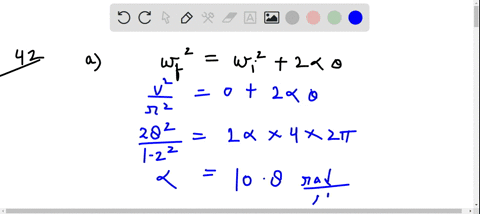
Solved A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg From A hammer thrower accelerates the hammer (mass = 7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate. (10 53) a hammer thrower accelerates the hammer (mass = 7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of.

Solved A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg From (iii) a hammer thrower accelerates the hammer of mass 7.30 kg (fig. 10 64 므) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s. assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential. For our hammer thrower, the angular acceleration can be found using the relationship between angular velocity and displacement, given by: initial angular velocity \( = 0 \) (since it starts from rest) the hammer makes four complete revolutions (i.e., \(4 \times 2\pi\) radians). Step 1: calculate the angular velocity (\ (\omega\)) at the time of release. since the hammer is released at a speed (v) of 26.5 m s and follows a circular path of radius (r) 1.20 m, use the formula \ (\omega = \frac {v} {r}\). step 2: determine the angular acceleration (\ (\alpha\)). Assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force being exerted on the hammer by the athlete just before release, and (e) the angle of thi.

Solved A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg From Step 1: calculate the angular velocity (\ (\omega\)) at the time of release. since the hammer is released at a speed (v) of 26.5 m s and follows a circular path of radius (r) 1.20 m, use the formula \ (\omega = \frac {v} {r}\). step 2: determine the angular acceleration (\ (\alpha\)). Assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force being exerted on the hammer by the athlete just before release, and (e) the angle of thi. Assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force being exerted on the hammer by the athlete just before release, and (e) the angle of thi. With a hammer mass of \( 7.30 \text{ kg} \) and the tangential acceleration at \( 13.08 \text{ m s}^2 \), the net force equates to \( 7.30 \times 13.08 \approx 95.48 \text{ n} \). this result conveys the effective push exerted by the thrower to maintain and increase the hammer's speed throughout the throw. Calculate the centripetal acceleration just before release. calculate the net force being exerted on the hammer by the athlete just before release. ignore gravity. calculate the angle of this force with respect to the radius of the circular motion. here’s the best way to solve it. to solve this problem, we need to use the relation. (iii) a hammer thrower accelerates the hammer (mass =7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the.

Solved A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg From Assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the centripetal acceleration just before release, (d) the net force being exerted on the hammer by the athlete just before release, and (e) the angle of thi. With a hammer mass of \( 7.30 \text{ kg} \) and the tangential acceleration at \( 13.08 \text{ m s}^2 \), the net force equates to \( 7.30 \times 13.08 \approx 95.48 \text{ n} \). this result conveys the effective push exerted by the thrower to maintain and increase the hammer's speed throughout the throw. Calculate the centripetal acceleration just before release. calculate the net force being exerted on the hammer by the athlete just before release. ignore gravity. calculate the angle of this force with respect to the radius of the circular motion. here’s the best way to solve it. to solve this problem, we need to use the relation. (iii) a hammer thrower accelerates the hammer (mass =7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the.
Solved Iii A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg Calculate the centripetal acceleration just before release. calculate the net force being exerted on the hammer by the athlete just before release. ignore gravity. calculate the angle of this force with respect to the radius of the circular motion. here’s the best way to solve it. to solve this problem, we need to use the relation. (iii) a hammer thrower accelerates the hammer (mass =7.30 kg) from rest within four full turns (revolutions) and releases it at a speed of 26.5 m s assuming a uniform rate of increase in angular velocity and a horizontal circular path of radius 1.20 m, calculate (a) the angular acceleration, (b) the (linear) tangential acceleration, (c) the.
Solved Iii A Hammer Thrower Accelerates The Hammer Mass 7 30 Kg
