Solved In Exercise Let A 1 2 3 4 5 6 And P1 1 2 Chegg

Solved In Exercise Let A 1 2 3 4 5 6 And P1 1 2 Chegg Question: in exercise, let a = {1, 2, 3, 4, 5, 6} and p1 = 1 2 3 4 5 6 3 4 1 2 6 5 p2 = 1 2 3 4 5 6 2 3 1 5 4 6 🙂 1) p3 = 1 2 3 2 3 4 5 6 6 3 2 5 4 1 compute (a) (p20 p.) 2 (b) pio (p3 0 pz). It is quite straightforward to check that ⊆ ⊆ is a partial order. now, r r works on pairs rather than elements, and the general schema that r r follows is called the lexicographic order. the only thing we would like to do is check if it really is a partial order: let ≤x ≤ x and ≤y ≤ y be partial orders on x x and y y respectively.

Solved Let A 5 3 6 2 0 1 1 4 3 B 2 5 1 3 8 Chegg Step 3: depict the relation using an arrow diagram to create an arrow diagram, we will represent the elements of set a on both sides and draw arrows from each x to y based on the pairs in the relation r. Define a relation r from a to a by r = { (x, y) : y = x 1 } depict this relation using an arrow diagram. it is given that y = x 1 also, x, y ∈ a r = { (1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}. For the partition sub sets to be an equivalence relation, the following conditions must be met: the partition sub sets must be distinct, meaning they must not share any entries. Exercise 7. let a = {1,2,3,4,5,6}. in each case (i) (iii) give an example of a relation on the set a with the given properties. the relations can be described by listing the ordered pairs or by a formula. clearly explain your solutions. if such a relation doesn’t exist, give a reason.

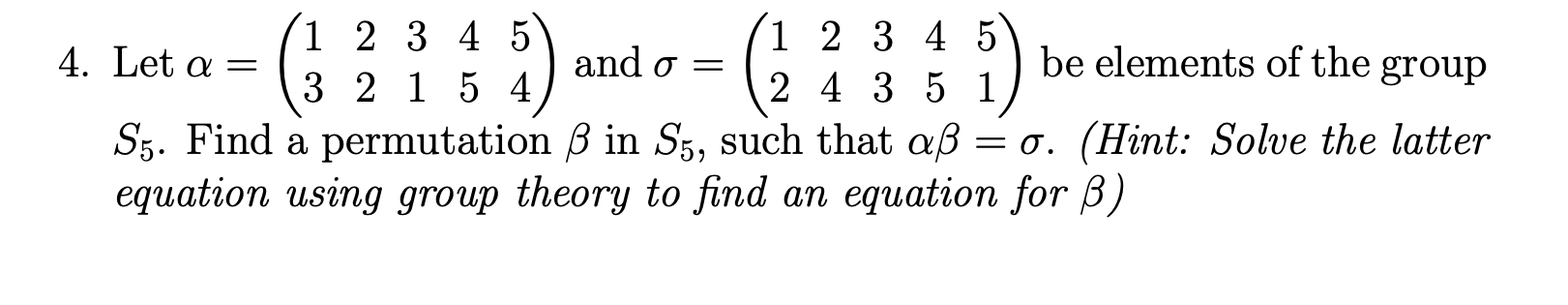
Solved 1 2 3 4 5 1 2 3 4 5 4 Let A And O 2 ñ 1 Be Chegg For the partition sub sets to be an equivalence relation, the following conditions must be met: the partition sub sets must be distinct, meaning they must not share any entries. Exercise 7. let a = {1,2,3,4,5,6}. in each case (i) (iii) give an example of a relation on the set a with the given properties. the relations can be described by listing the ordered pairs or by a formula. clearly explain your solutions. if such a relation doesn’t exist, give a reason. Since a = {a, b, c, d} has 4 elements and b = {1, 2, 3, 4, 5, 6} has 6 elements in it, the total number of one to one functions possible is: = (6 possibilities for mapping a) × (5 possibilities for mapping b) × (4 possibilities for mapping c) × (3 possibilities for mapping d) = 360. (iii) {5, 25, 125, 625} (iv) {2, 4, 6 upto infinity} (v) {1, 4, 9, upto 100} q: write the following sets in roster form: (i) a = {x: x is an integer and 3 < x < 7}. (ii) b = {x: x is a natural number less than 6}. (iii) c = {x: x is a two digit natural number such that the sum of its digits is 8} (iv) d = {x: x is a prime number which is. Let a = {1, 2, 3, 4, 5, 6} and let r = { (1, 1), (1, 2), (1, 3), (1, 4), (2, 3), (2, 5), (2, 6), (3, 5), (4, 5), (4, 6)}. (a) give an example of elements a, b ∈ a such that arb. Our expert help has broken down your problem into an easy to learn solution you can count on. question: let a = {1,2,3,4,5,6} and p: a abe a permutation function on a. suppose that p 1 2 3 4 5 6 4 1 6 5 2 3 3) for the following questions. (see directions at the end of the question.).