Solved Let A 1 0 1 2 1 1 3 1 0 And B 0 0 1 1 1 1 Chegg

Solved Let B 1 0 1 0 1 1 1 1 0 And B Chegg There are 4 steps to solve this one. the matrix a, b, c, d are given here. (a) find the multiplication a d as follows. the product is a d = [4 10 9 1 2 9 5 8 15 5 8 8 4 8 1]. Solution: since square a matrix is invertible if and only if elimination yields the same number of pivots as rows, we just need to do elimination on a and b and see what conditions on their entries ensure that we get a pivot in every row.

Solved Let B 1 1 0 0 1 1 1 0 1 And B 1 Chegg For the system of linear equations: x − 2y = 1, x − y kz = −2, ky 4z = 6,k ∈ r consider the following statements: (a) the system has unique solution if k ≠ 2,k ≠ −2 (b) the system has unique solution if k = 2. (c) the system has unique solution if k = 2. (d) the system has no solution if k = 2. If \ (\alpha=|\mathrm {b}|\) and \ (\beta\) is the sum of all the diagonal elements of \ (\mathrm b\), then \ (\alpha^ {3} \beta^ {3}\) is equal to . Ask yourself if the three form a linearly independent set using known techniques (e.g. row reducing). conclude that since you have three linearly independent vectors in a three dimensional space, they must span the whole space. Here, sets a and b are given, and we're asked to find several different cartesian products. in general, the cartesian product (denoted by 'x') of two sets, say a and b, is the set of all ordered pairs where the first element is from a and the second element is from b.
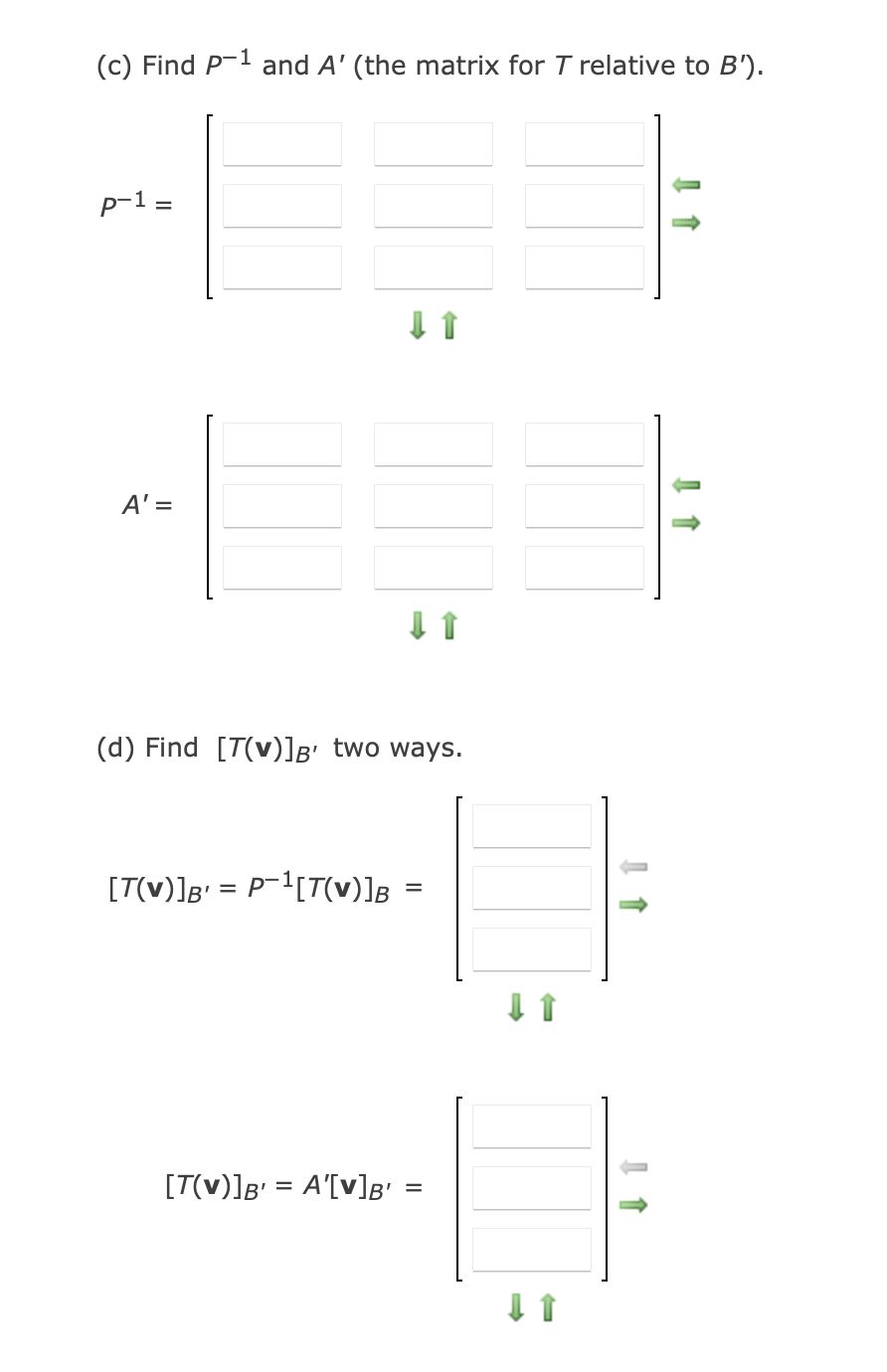
Solved Let B 0 1 1 1 1 0 1 0 1 And B Chegg Ask yourself if the three form a linearly independent set using known techniques (e.g. row reducing). conclude that since you have three linearly independent vectors in a three dimensional space, they must span the whole space. Here, sets a and b are given, and we're asked to find several different cartesian products. in general, the cartesian product (denoted by 'x') of two sets, say a and b, is the set of all ordered pairs where the first element is from a and the second element is from b. Step by step video & image solution for let a = [ [1,0,0], [0,1,1], [1,1,1]] and b=a^20. then the sum of the elements of the first column of b is : by maths experts to help you in doubts & scoring excellent marks in class 12 exams. Let a = \ (\begin {pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end {pmatrix}\) and b = 7a20 20a7 2i, where i is an identity matrix of order 3 × 3. if b = [bij], then b13 is equal to . Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. ask me … not the question you’re looking for? post any question and get expert help quickly. To solve the problem, we will follow these steps: we are given that tr(a) =7. therefore, we can set up the equation: this is a quadratic function in b which opens downwards (since the coefficient of b2 is negative). the maximum value occurs at the vertex, given by:.

Solved Let B 0 1 1 1 1 0 1 0 1 And B Chegg Step by step video & image solution for let a = [ [1,0,0], [0,1,1], [1,1,1]] and b=a^20. then the sum of the elements of the first column of b is : by maths experts to help you in doubts & scoring excellent marks in class 12 exams. Let a = \ (\begin {pmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end {pmatrix}\) and b = 7a20 20a7 2i, where i is an identity matrix of order 3 × 3. if b = [bij], then b13 is equal to . Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. ask me … not the question you’re looking for? post any question and get expert help quickly. To solve the problem, we will follow these steps: we are given that tr(a) =7. therefore, we can set up the equation: this is a quadratic function in b which opens downwards (since the coefficient of b2 is negative). the maximum value occurs at the vertex, given by:.
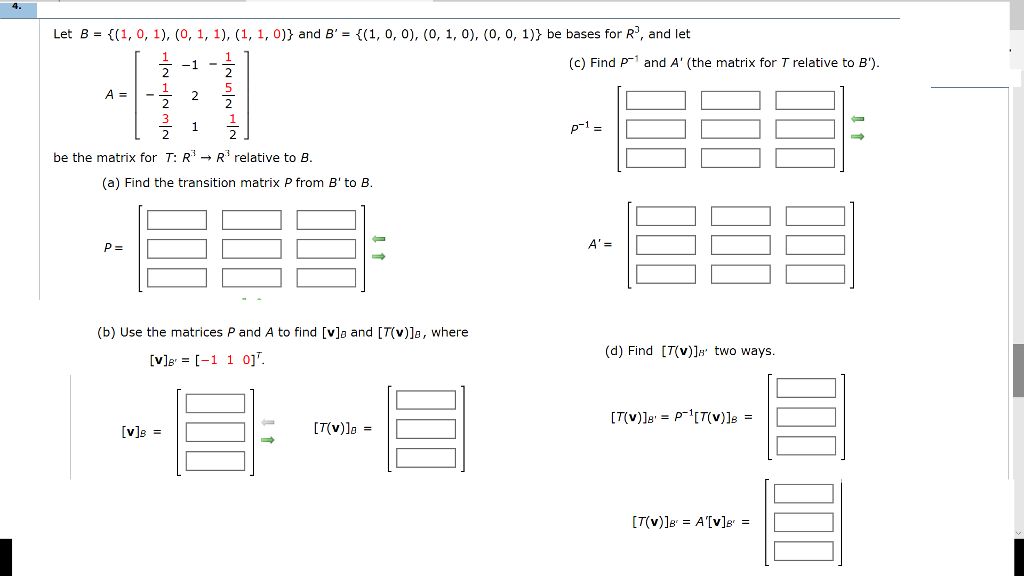
Solved Let B 1 0 1 0 1 1 1 1 0 And B Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. ask me … not the question you’re looking for? post any question and get expert help quickly. To solve the problem, we will follow these steps: we are given that tr(a) =7. therefore, we can set up the equation: this is a quadratic function in b which opens downwards (since the coefficient of b2 is negative). the maximum value occurs at the vertex, given by:.
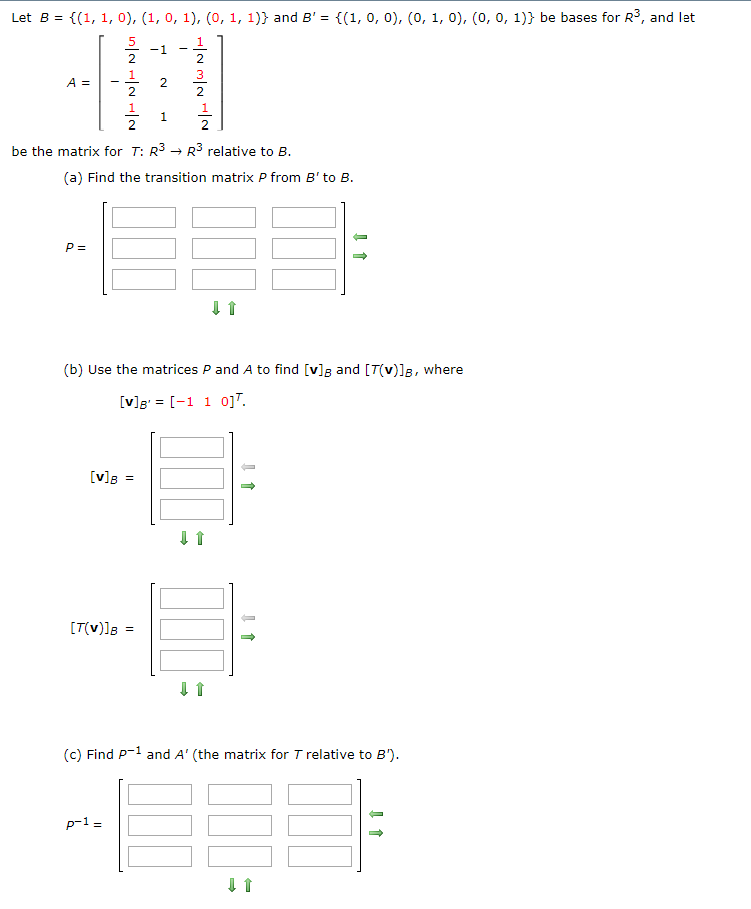
Solved Let B 1 1 0 1 0 1 0 1 1 And B Chegg
Comments are closed.