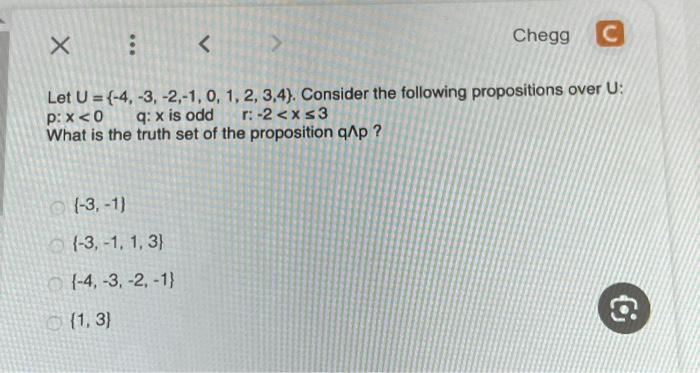
Solved Chegg C Let U 4 3 2 1 0 1 2 3 4 Consider Chegg Let a = b = {1, 2, 3}, and consider the function f: a → b defined as follows: f(1) = 3, f(2) = 1, f(3) = 3. a. f is onto only. b. f is one to one only. c. f is one to one correspondence. d. f is neither one to one nor onto. There are 4 steps to solve this one. the function (f: a → a) is defined as (f (x) = x). this function is one to one be not the question you’re looking for? post any question and get expert help quickly. answer to let a = {1, 2, 3} and b = {a, b, c, d}. give an.
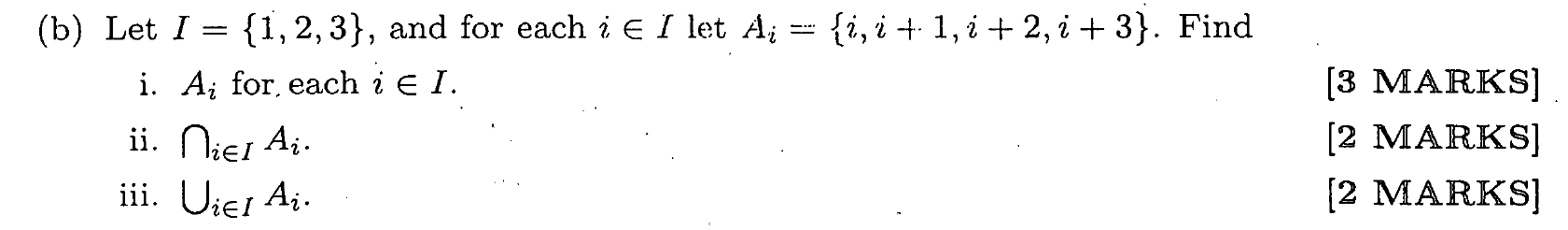
Solved B Let I 1 2 3 And For Each Iв I Let Chegg To determine the properties of the relation $$r$$r defined on the set $$a = \ { 1, 2, 3 \}$$a= {1,2,3}, we first need to establish what $$r$$r is. the relation $$r$$r is defined as the cartesian product $$a \times a$$a×a, which consists of all ordered pairs where both elements are from the set $$a$$a. check for reflexivity. Let a = {1, 2, 3}. consider the function f = {(1,2), (2,3), (3,1)} on set a. which of the following is true? of 1 = {(2, 1), (3, 2), (3, 1)} on != {(1, 2), (2,3), (3,1)} 2 of 1 = {(2, 1), (3, 1), (1,3)} the inverse function f 1 does not exist. Misc 7 let a = {1, 2, 3}. then number of equivalence relations containing (1, 2) is (a) 1 (b) 2 (c) 3 (d) 4 total possible pairs = { (1, 1) , (1, 2), (1, 3), (2, 1) , (2, 2), (2, 3), (3, 1) , (3, 2), (3, 3) } reflexive means (a, a) should be in relation . Examples: $\{1,2,3,4,5\} = \{5,2,1,3,4\}$. both are the same sets, defined simply by the elements they contain, and no more. on the other hand, for tuples, the order of elements within the tuple is definitive. think of coordinates! when you write $(x,y)$, order obviously matters: on a grid, the point $(2,4)$ is not equal to the point $(4,2)$.

Let 1 2 3 4 2 And Let Chegg Misc 7 let a = {1, 2, 3}. then number of equivalence relations containing (1, 2) is (a) 1 (b) 2 (c) 3 (d) 4 total possible pairs = { (1, 1) , (1, 2), (1, 3), (2, 1) , (2, 2), (2, 3), (3, 1) , (3, 2), (3, 3) } reflexive means (a, a) should be in relation . Examples: $\{1,2,3,4,5\} = \{5,2,1,3,4\}$. both are the same sets, defined simply by the elements they contain, and no more. on the other hand, for tuples, the order of elements within the tuple is definitive. think of coordinates! when you write $(x,y)$, order obviously matters: on a grid, the point $(2,4)$ is not equal to the point $(4,2)$. If we add (2, 3), we need to add (3, 2) for symmetric, but it would become transitive then relation r1 = { so, there is only 1 possible relation correct answer is a. show more chapter 1 class 12 relation and functions. Let a = {1,2,3} and b = {a, b, c, d]. give an example of the following. if you think no such example exists, you must explain why not. you may not use any examples from elsewhere in this assignment. (hint: only four of these are impossible.) for parts (a) (), you should use set list notation or a directed graph. Our expert help has broken down your problem into an easy to learn solution you can count on. question: 1a. let a= {1,2,3}. write out all elements of a×a. list two examples of relations on the set a= {1,2,3}, one which is not a function and one which is a function. 1b. construct three different partitions of the integers. 1a. let a= {1,2,3}. Theorem 1 (algebraic operations of matrices) let a, b, c be matrices of appropriate sizes. (c) there exists a unique c such that a c = o and we denote c = −a. 2. multiplication: (a b)c = ac bc and c(a b) = ca cb. 3. transpose: (a b)> = a> b>. (ab)> = b>a>. (ka)> = ka>. example 2 calculate (abc)> using the following matrices.

Solved Let A 0 1 2 3 And Let Chegg If we add (2, 3), we need to add (3, 2) for symmetric, but it would become transitive then relation r1 = { so, there is only 1 possible relation correct answer is a. show more chapter 1 class 12 relation and functions. Let a = {1,2,3} and b = {a, b, c, d]. give an example of the following. if you think no such example exists, you must explain why not. you may not use any examples from elsewhere in this assignment. (hint: only four of these are impossible.) for parts (a) (), you should use set list notation or a directed graph. Our expert help has broken down your problem into an easy to learn solution you can count on. question: 1a. let a= {1,2,3}. write out all elements of a×a. list two examples of relations on the set a= {1,2,3}, one which is not a function and one which is a function. 1b. construct three different partitions of the integers. 1a. let a= {1,2,3}. Theorem 1 (algebraic operations of matrices) let a, b, c be matrices of appropriate sizes. (c) there exists a unique c such that a c = o and we denote c = −a. 2. multiplication: (a b)c = ac bc and c(a b) = ca cb. 3. transpose: (a b)> = a> b>. (ab)> = b>a>. (ka)> = ka>. example 2 calculate (abc)> using the following matrices.
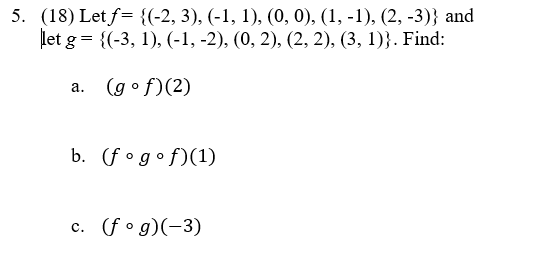
Solved Let F 2 3 1 1 0 0 1 1 2 3 Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: 1a. let a= {1,2,3}. write out all elements of a×a. list two examples of relations on the set a= {1,2,3}, one which is not a function and one which is a function. 1b. construct three different partitions of the integers. 1a. let a= {1,2,3}. Theorem 1 (algebraic operations of matrices) let a, b, c be matrices of appropriate sizes. (c) there exists a unique c such that a c = o and we denote c = −a. 2. multiplication: (a b)c = ac bc and c(a b) = ca cb. 3. transpose: (a b)> = a> b>. (ab)> = b>a>. (ka)> = ka>. example 2 calculate (abc)> using the following matrices.
