Solved Let A A B C D E F G H I And B 2a 2b 2c A G Chegg
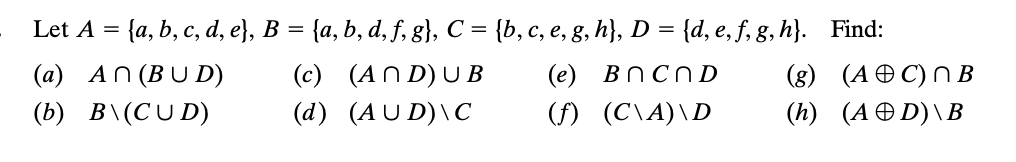
Solved Let Chegg Question: letdet [ [a,b,c], [d,e,f], [g,h,i]]= 2calculate the following determinants without expanding them:det [ [2a,2b,2c], [g 3d,h 3e,i 3f], [d,e,f]], and ,det [ [d e,a b,g h], [e f,b c,h i], [e f,b c,h i]]. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. The correct answer is: (a−b)∪(b−a)= |b,c,e,f,g,h|. to solve the problem, we need to find the sets a−b and b−a, and then take the union of these two sets. thus, a−b={b,e,f}. thus, b−a={c,g,h}. the union (a−b)∪(b−a) contains all the elements that are in either a−b or b−a. thus, (a−b)∪(b−a) ={b,e,f,c,g,h}.

Solved If Det A B C D E F G H I 7 Then Find A D E F Chegg In set theory, the operation a b (read as 'a minus b' or 'a without b') indicates all elements of the set a that are not found in the set b. this operation is also known as the relative complement or difference of b in a. Step 1: find the complement of set c to find the complement of set c with respect to the universal set u, we need to find all the elements in u that are not in c. In our exercise, we are finding the intersection of set b and the complement of set c. this operation filters through both sets and identifies the items that they share in this case, the letters b and g are the shared elements, leading to the intersection set containing these two letters. Let a = {a, b, c, d, e) and b = {a, b, c, d, e, f, g, h}. match the given sets in the left to the sets in the right. 1 b a 2 a b 3 aub 4 anb match each of the options above to the items below. {a, b, c, d, e, f, g, h} {a, b, c, d, e) 0 {f, g, h} your solution’s ready to go!.
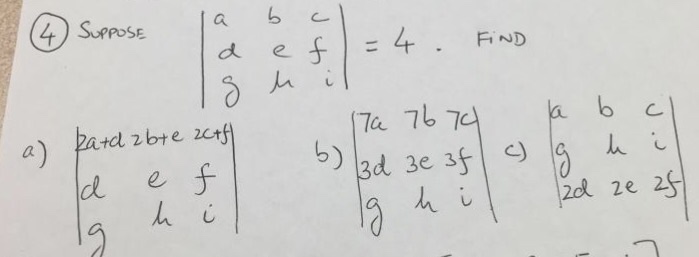
Solved Suppose A B C D E F G H I 4 Find 2a D 2b Chegg In our exercise, we are finding the intersection of set b and the complement of set c. this operation filters through both sets and identifies the items that they share in this case, the letters b and g are the shared elements, leading to the intersection set containing these two letters. Let a = {a, b, c, d, e) and b = {a, b, c, d, e, f, g, h}. match the given sets in the left to the sets in the right. 1 b a 2 a b 3 aub 4 anb match each of the options above to the items below. {a, b, c, d, e, f, g, h} {a, b, c, d, e) 0 {f, g, h} your solution’s ready to go!. @whipcored while this is a method to solve it, i'd recommend against it. the power of this method is that it will work for any matrix with $\det a = 7$, not just the specific one you wrote down. Let $a=\ {\mathbf {a}, \mathbf {b}, \mathbf {c}, \mathbf {d}, \mathbf {e}\}, b= (\mathbf {d}, \mathbf {e}, \mathbf {f}, \mathbf {g}\},$ and $c=\ {\mathbf {a}, \mathbf {c}, \mathbf {e}, \mathbf {f}\} .$ find each set. Buc is the union of the two sets b and c. the union contains all the elements that belong to b or c (or both). so in this case, it would be (a,g,i,j,k,e,h) a b is a modification of a set by removing the elements of b from the set a. so a b= {b,c,d,e,f) while (a b) c= {b,c,d,f} still looking for help? get the right answer, fast. Sol: the set b is the empty set ∅. if there were any elements in b that were also in a, then these elements would not be in the symmetric difference and the symmetric difference could not contain all of a.
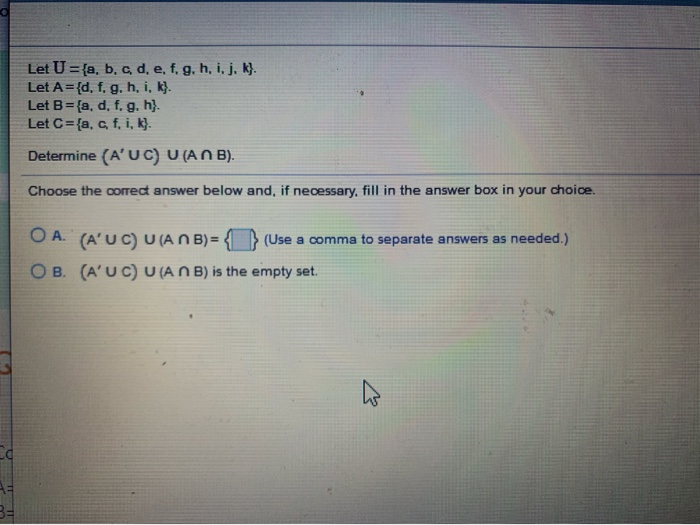
Solved Let U A B C D E F G H I J K Let A D Chegg @whipcored while this is a method to solve it, i'd recommend against it. the power of this method is that it will work for any matrix with $\det a = 7$, not just the specific one you wrote down. Let $a=\ {\mathbf {a}, \mathbf {b}, \mathbf {c}, \mathbf {d}, \mathbf {e}\}, b= (\mathbf {d}, \mathbf {e}, \mathbf {f}, \mathbf {g}\},$ and $c=\ {\mathbf {a}, \mathbf {c}, \mathbf {e}, \mathbf {f}\} .$ find each set. Buc is the union of the two sets b and c. the union contains all the elements that belong to b or c (or both). so in this case, it would be (a,g,i,j,k,e,h) a b is a modification of a set by removing the elements of b from the set a. so a b= {b,c,d,e,f) while (a b) c= {b,c,d,f} still looking for help? get the right answer, fast. Sol: the set b is the empty set ∅. if there were any elements in b that were also in a, then these elements would not be in the symmetric difference and the symmetric difference could not contain all of a.
Comments are closed.