
Solved Let A R Prove That A A 0 If And Only If A Chegg Solution; let a, b ∈ r, now if a 2 b 2 = 0 then we have to show that a = b = 0. since we know that (a b) 2 = a 2 b 2 2 a b. Let p = {a∈ r: a>0}. for any a∈ r, taking b= 0 in (p10′), we see that exactly one of the following is true: either a<0, or a= 0, or 0

Solved Let A Bв R Prove That A2 B2 0 If And Only If A B 0 Chegg Let a;b2r and suppose that for every ">0, we have a b ". show that a b. solution assume that a>b, i.e. a b>0 and choose "= a b 2. then, by the hypothesis, a b a b 2, a 2 b 2,a b, a contradiction. hence, a b. 3 prove that for any a;b2r: (a b 2)2 a2 b2 2 show that equality holds if and only if a = b. solution let a;b2r. then, by expanding. Since 0 0. by the multiplication law, a < b implies ab < b2. using the transitive law again, a2

Use The Fact Above To Prove That Dε 0 R R 0 Chegg If $ab = 0$ then $a = 0$ or $b=0$ proof. let $a, b \in \mathbb{r}$ with $ab =0$ then, if $a \neq 0$ we know there exists $a^{ 1} \in \mathbb{r}$ such that $a * a^{ 1} = 1$ thus, $$\begin{align} ab = 0 &\implies a^{ 1}(ab) = a^{ 1} \cdot 0 = 0\tag{1}\label{1} \\ \end{align}$$ but,. Prove: if x is an accumulation points of the set s, then every neighborhood of x contains infinitely many points of s. let x∈s'. then n* (x)∩s≠Ø. let xn be an element of the ε n neighborhood. then there are infinite xns contained in n (x) and s. proof by contradiction. then n (x,ε)∩s=Ø which is a condridiction. 21. When a sum comprises non negative terms, the sum being zero implies that each individual term must be zero. this principle is central to the proof that the sum of squares of real numbers being zero forces each of the original numbers to be zero. a biconditional proof involves establishing both the forward and reverse implications. A biconditional proof involves establishing both the forward and reverse implications. in this context, it requires showing that if the sum of the squares is zero, then each variable is zero, and vice versa, thereby reinforcing the equivalence between the conditions. Let a,b,c,d∈r. prove that (a) if a≤b and c≤d, then a c≤b d. (b) if a≤b and c0, then −a<0. (d) if a>0 and b>0, then ab>0. (e) if a0, then ac your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: real numbers. let a,b,c,d∈r. Prove that a2 − b2 = (a b)(a − b) for all a, b ∈ r if and only if r is commutative. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
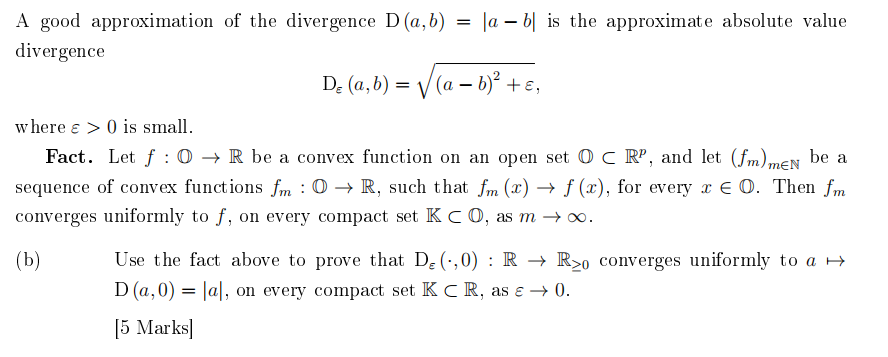
Use The Fact Above To Prove That Dε 0 R R 0 Chegg When a sum comprises non negative terms, the sum being zero implies that each individual term must be zero. this principle is central to the proof that the sum of squares of real numbers being zero forces each of the original numbers to be zero. a biconditional proof involves establishing both the forward and reverse implications. A biconditional proof involves establishing both the forward and reverse implications. in this context, it requires showing that if the sum of the squares is zero, then each variable is zero, and vice versa, thereby reinforcing the equivalence between the conditions. Let a,b,c,d∈r. prove that (a) if a≤b and c≤d, then a c≤b d. (b) if a≤b and c0, then −a<0. (d) if a>0 and b>0, then ab>0. (e) if a0, then ac your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: real numbers. let a,b,c,d∈r. Prove that a2 − b2 = (a b)(a − b) for all a, b ∈ r if and only if r is commutative. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved Let A B C D R Prove That If A B 0 And C D Chegg Let a,b,c,d∈r. prove that (a) if a≤b and c≤d, then a c≤b d. (b) if a≤b and c0, then −a<0. (d) if a>0 and b>0, then ab>0. (e) if a0, then ac your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: real numbers. let a,b,c,d∈r. Prove that a2 − b2 = (a b)(a − b) for all a, b ∈ r if and only if r is commutative. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved 4 Prove The Following Theorem Let A And B Be Given Chegg
