
Solved B Let F Be The Ordered Basis Of R Given By 3 Chegg There are 2 steps to solve this one. let b = { (1.2). ( 3.1)} be a (ordered) basis for r2. and let e = { (1,0). (0.1)} be the standard busies. Find the coordinate vector of v = (1,0) with respect to b. 1 3 (a) [v]b = (b) [v]b = 2 3 (c) [v]b = 3 2 3 (d) [v]b (e) [v]b 3 2 1. here’s the best way to solve it. 6. let b be the following ordered basis for r2: В. { (1, 1), (2, 3)} .
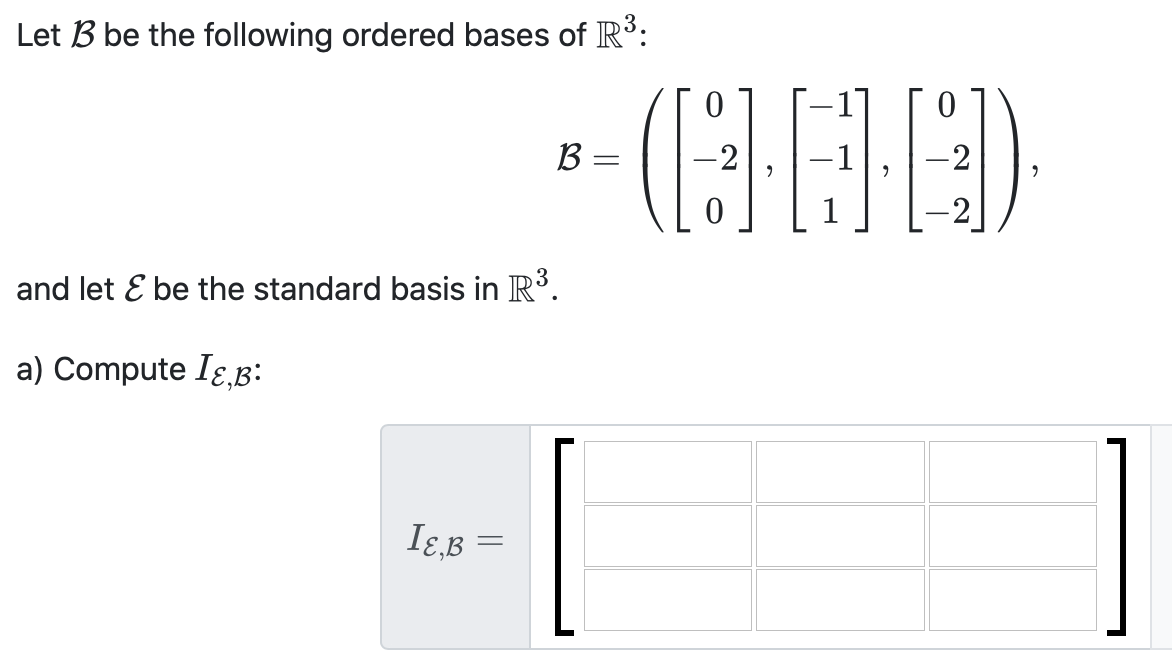
Solved Let B Be The Following Ordered Bases Of R3 0 Chegg Consider the ordered basis b = ( ( [11] [1]) of r? of r2. let t: r2 r2 be the linear . transformation such that [3 0 tbb = = 18] pute t (v). enter your answer in the standard basis for r2, not in the b let v= basis. 6 t (v) = = [ x 0% 6. your solution’s ready to go!. Solution: first let dim(n(t))=k. by the dimension formula this implies that dim(r(t))=n − k. let {β1, β2, , βk} be a basis for the subspace n(t). now let γr(t)={γk 1, γk 2, , γn} be a basis for the subspace, r(t); we note that this set has n − k elements. Let $t$ be the linear operator on $r^2$ defined by $t (x 1,x 2)= ( x 2,x 1)$. (d) prove that if $b$ is any ordered basis for $r^2$ and $ [t] b = a$, then $a {12}\cdot a {21}\neq 0$. Let β be the standard ordered basis for r2 and γ = { (1, 1, 0), (0, 1, 1), (2, 2, 3) }. compute [t]γ β. if α = { (1, 2), (2, 3) }, compute [t]γ α. idea: the general approach to compute [t]β is to compute t(v) for all v ∈ α, then represent these vectors in α β coordinate. the matrix [t]β isthenformedbyarrangingthecoe傉ᄷcientsappropriately. 2.2.5.
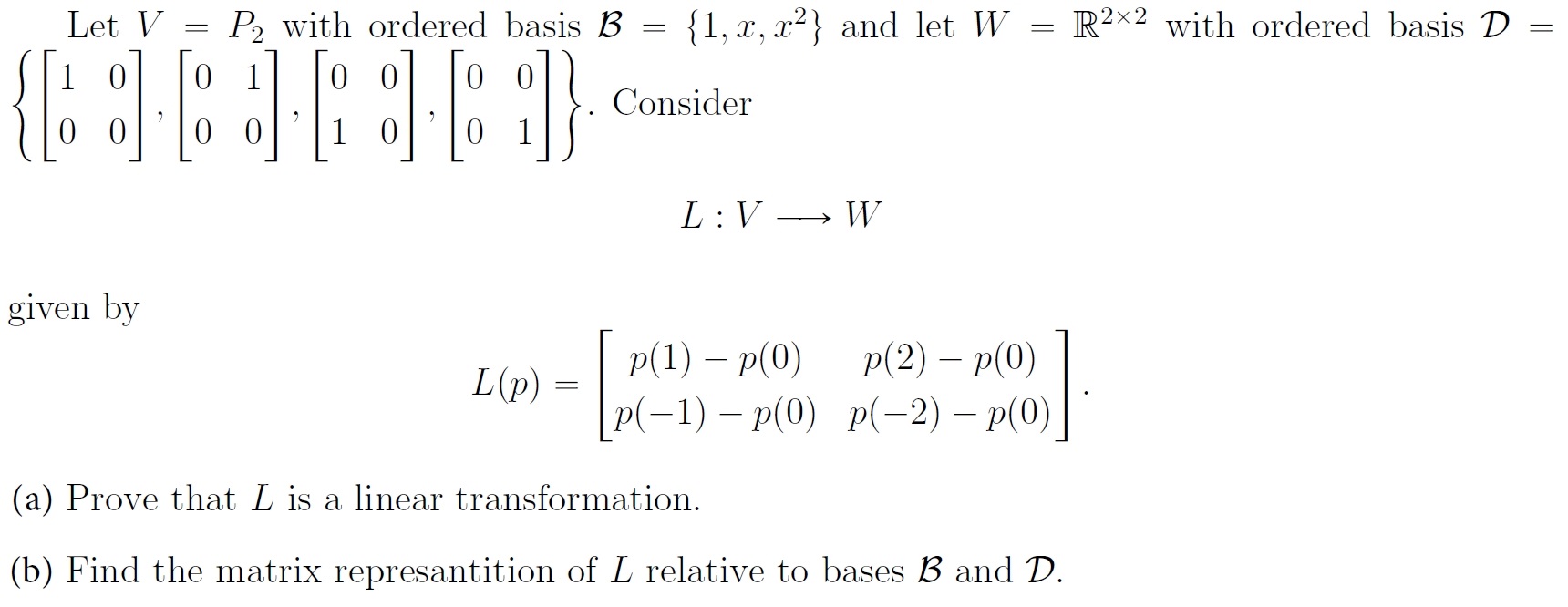
Solved Let V P2 With Ordered Basis B 1 X X2 And Let W R2 2 Chegg Let $t$ be the linear operator on $r^2$ defined by $t (x 1,x 2)= ( x 2,x 1)$. (d) prove that if $b$ is any ordered basis for $r^2$ and $ [t] b = a$, then $a {12}\cdot a {21}\neq 0$. Let β be the standard ordered basis for r2 and γ = { (1, 1, 0), (0, 1, 1), (2, 2, 3) }. compute [t]γ β. if α = { (1, 2), (2, 3) }, compute [t]γ α. idea: the general approach to compute [t]β is to compute t(v) for all v ∈ α, then represent these vectors in α β coordinate. the matrix [t]β isthenformedbyarrangingthecoe傉ᄷcientsappropriately. 2.2.5. Solution 1.7.2.3 1.7.2. 3 1.7.2.9 1.7.2. 9 solution now we show how to find bases for the column space of a matrix and the null space of a matrix. in order to find a basis for a given subspace, it is usually easiest to rewrite the subspace as a column space or a null space first. first we show how to compute a basis for the column space of a. Dim[symn( r) ] dim [skewn( r) ] = dim [mn( r) ]. for problems 32–34, a subspace s of a vector space v is given. determine a basis for s and extend your basis for s 35. let s be a basis for pn −1. prove that s ∪{xn } is a basis for pn. to obtain a basis for v . 32. v 3, s is the subspace consisting of all points r =. Let v be a finite dimensional vector space. [x]b is also known as the b coordinate vector of x. c1; c2; : : : ; cn are also known as the b coordinates of x. the order of the vectors in the basis is critical, hence the term ordered basis. recall the standard bases for common vector spaces: dim. Consider the ordered bases b = { [−7, 6], [1, −1]} and c = { [2, −3], [4, 4]} for the vector space r². find the transition matrix from c to the standard ordered basis e= { [1, 0], [0, 1]}.

Solved 19 Let B V1 V2 V3 Be The Ordered Basis Of R3 Chegg Solution 1.7.2.3 1.7.2. 3 1.7.2.9 1.7.2. 9 solution now we show how to find bases for the column space of a matrix and the null space of a matrix. in order to find a basis for a given subspace, it is usually easiest to rewrite the subspace as a column space or a null space first. first we show how to compute a basis for the column space of a. Dim[symn( r) ] dim [skewn( r) ] = dim [mn( r) ]. for problems 32–34, a subspace s of a vector space v is given. determine a basis for s and extend your basis for s 35. let s be a basis for pn −1. prove that s ∪{xn } is a basis for pn. to obtain a basis for v . 32. v 3, s is the subspace consisting of all points r =. Let v be a finite dimensional vector space. [x]b is also known as the b coordinate vector of x. c1; c2; : : : ; cn are also known as the b coordinates of x. the order of the vectors in the basis is critical, hence the term ordered basis. recall the standard bases for common vector spaces: dim. Consider the ordered bases b = { [−7, 6], [1, −1]} and c = { [2, −3], [4, 4]} for the vector space r². find the transition matrix from c to the standard ordered basis e= { [1, 0], [0, 1]}.

Solved Let Bвѓ 1 в 12 And Bвѓ 2 в 23 The Set B Bвѓ 1 Bвѓ 2 Chegg Let v be a finite dimensional vector space. [x]b is also known as the b coordinate vector of x. c1; c2; : : : ; cn are also known as the b coordinates of x. the order of the vectors in the basis is critical, hence the term ordered basis. recall the standard bases for common vector spaces: dim. Consider the ordered bases b = { [−7, 6], [1, −1]} and c = { [2, −3], [4, 4]} for the vector space r². find the transition matrix from c to the standard ordered basis e= { [1, 0], [0, 1]}.
