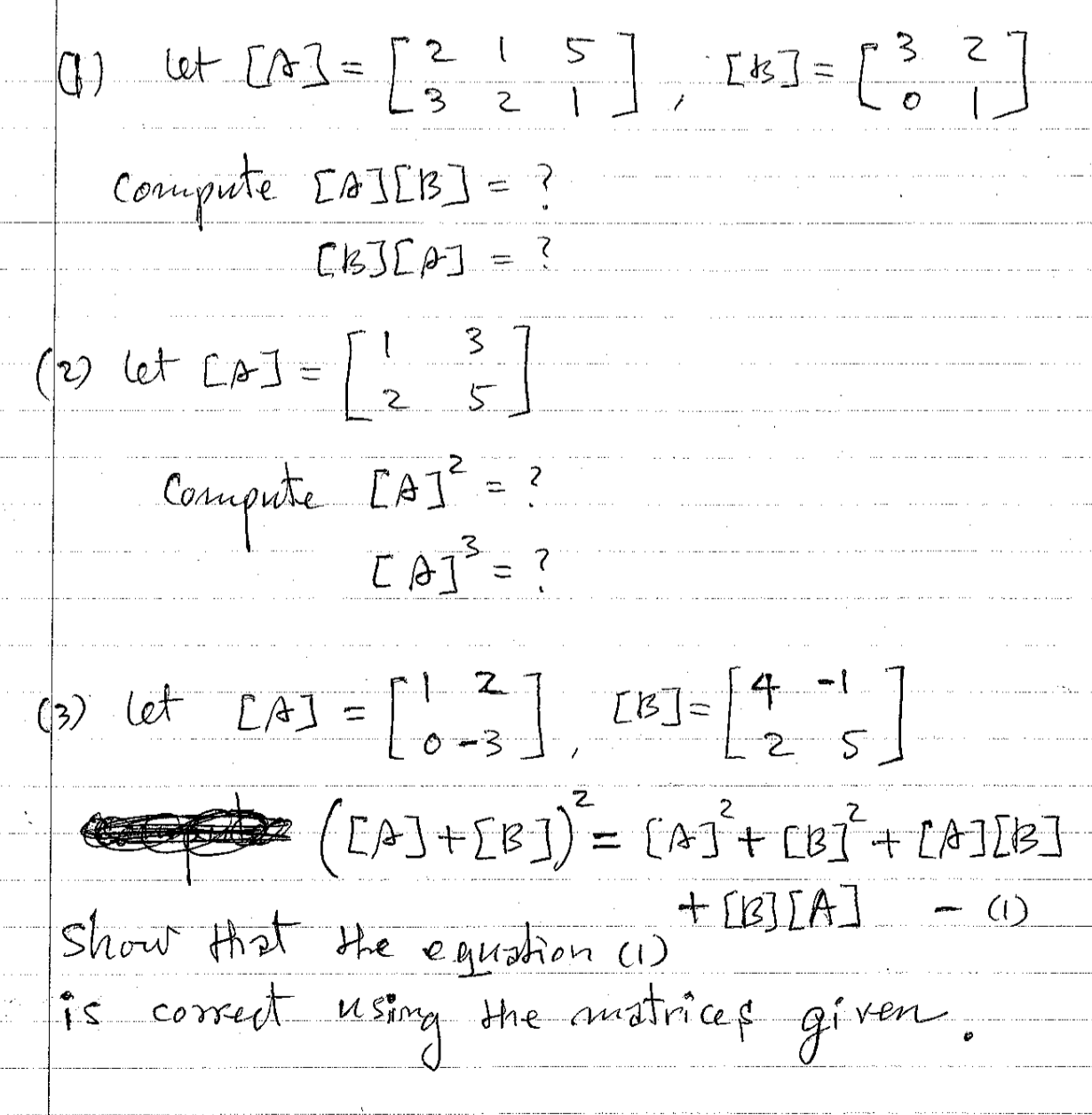
Solved Let A 2 1 5 3 2 1 B 3 2 0 1 Compute Chegg There are 2 steps to solve this one. exercise 1. let a={1,2,3,4,5} and b ={1,2,3,4,5}. consider the following relations: which of the following are one to one from a to b ? which of the following are onto from a to b ? a. Study with quizlet and memorize flashcards containing terms like let a = {1, 4, 5, 6, 7, 8} and b = {1, 5, 6}. indicate if each statement is true or false. 7∈a b⊂a, let u=u={1,2,3, ,10}, a=a={1,3,5,7}, b=b={1,2,3,4}, and c=c={3,4,6,7,9}.

Solved Let A 1 2 3 4 5 And B 0 3 6 Find A B Chegg The total number of functions, f : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} such that f(1) f(2) = f(3), is equal to q6. let ƒ(x) = x5 2ex 4 for all x ∈ r. consider a function g(x) such that (gof) (x) = x for all x ∈ r. Let a = {1, 2, 3, 4, 5} and b = {2, 4}. what is a ∩ b? the intersection of sets a and b, denoted as a ∩b, consists of the elements that are present in both sets. for the sets a = {1,2,3,4,5} and b = {2,4}, the intersection is a ∩ b = {2,4}. to find the intersection of two sets, we look for elements that are present in both sets. Let b = {1, 2, 3, 4, 5} and s = {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (3, 3), (4, 1), (4, 4), (5, 5)}. assume (without proof) that s is an equivalence relation on b . find the equivalence class of each element of b . Free math problem solver answers your algebra homework questions with step by step explanations.

Solved Let A 1 2 3 And B 3 4 5 Find Aв B A 1 2 3 4 5 Chegg Let b = {1, 2, 3, 4, 5} and s = {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (3, 3), (4, 1), (4, 4), (5, 5)}. assume (without proof) that s is an equivalence relation on b . find the equivalence class of each element of b . Free math problem solver answers your algebra homework questions with step by step explanations. See our solution for question 8e from chapter 5.4 from lay's linear algebra and its applications, 5th edition. let = {b1, b2, b3} be a basis for a vector space v. find t (3b1 4b2) when t is a linear transformation from v to v whose matrix relative to is. The given input in figure s4.1 1 can be expressed as linear combinations of xi[n], x 2[n], x3[n]. (b) using superposition, y 4[n] = 2yi[n] 2y 2[n] y3 [n], shown in figure s4.1 2. (c) the system is not time invariant because an input xi[n] xi[n 1] does not produce an output yi[n] yi[n 1]. the input x,[n] xi[n 11 is xi[n] . Let x and y be two n0 valued random variables such that x = y z, where. z is a bernoulli random variable with parameter p 2 (0; 1), independent of y . only one of the following statements is true. which one? e[(x y )z] = e[(x y )]e[z]. the correct answer is (c). false. simply take y = 0, so that y z = z and x z = 2z. false. take y = 0. Let a, b , and c be n × n matrices with a and c invertible. solve the equation abc = i − a for b . solution: b = a−1(i − a)c−1 . you can rewrite this in various ways – but i won’t. however, one must be careful since the matrices a, b , and c are not assumed to commute. 2.

Solved 5 Let A 1 2 3 4 5 6 And Let B1 1 3 5 And Chegg See our solution for question 8e from chapter 5.4 from lay's linear algebra and its applications, 5th edition. let = {b1, b2, b3} be a basis for a vector space v. find t (3b1 4b2) when t is a linear transformation from v to v whose matrix relative to is. The given input in figure s4.1 1 can be expressed as linear combinations of xi[n], x 2[n], x3[n]. (b) using superposition, y 4[n] = 2yi[n] 2y 2[n] y3 [n], shown in figure s4.1 2. (c) the system is not time invariant because an input xi[n] xi[n 1] does not produce an output yi[n] yi[n 1]. the input x,[n] xi[n 11 is xi[n] . Let x and y be two n0 valued random variables such that x = y z, where. z is a bernoulli random variable with parameter p 2 (0; 1), independent of y . only one of the following statements is true. which one? e[(x y )z] = e[(x y )]e[z]. the correct answer is (c). false. simply take y = 0, so that y z = z and x z = 2z. false. take y = 0. Let a, b , and c be n × n matrices with a and c invertible. solve the equation abc = i − a for b . solution: b = a−1(i − a)c−1 . you can rewrite this in various ways – but i won’t. however, one must be careful since the matrices a, b , and c are not assumed to commute. 2.
