Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg

By forhairstyles On Aug 24, 2025

Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg Find the change of coordinates matrix from f to d.\\nb. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Question (âˆ¼exercise 4.7.6) let d = {d1, d2, d3} and f = {f1, f2, f3} be bases for a 3 dimensional linear subspace v of r^n, and f1 = 2d1 d2 d3, f2 = 3d2 d3, and f3 = 3d1 2d3.

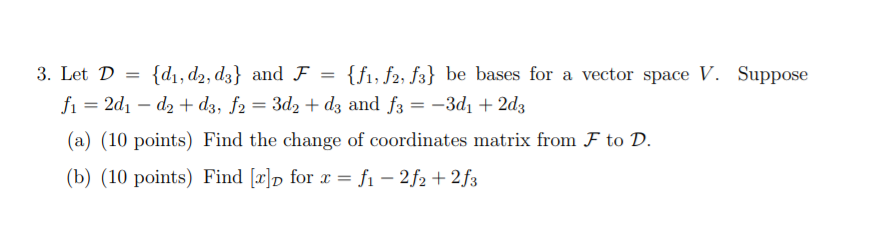
Solved 3 Let D Di D2 D3 And F F1 F2 F3 Be Bases Chegg Learn how to find the basis of a vector space using matrix operations. ask a question and one of our academic experts will send you an answer within hours. make sure to include all the information. Let d = {d 1, d 2, d 3} and f = {f 1, f 2, f 3} be bases for a vector space v, and suppose f 1 = 2d 1 d 2 d 3, f 2 = 3d 2 d 3, and f 3 = 3d 1 2d 3. a. find the change of coordinates matrix from f to d. b. find [x] d for x = f 1 2f 2 2f 3. Let d = {d 1, d 2, d 3} and f = {f 1, f 2, f 3} be bases for a vector space v, and suppose f 1 = 2d 1 d 2 d 3 f 2 = 3d 2 d 3, and f 3 = 3d 1 2d 3. a. find the change of coordinates matrix from f to d. b. find [x] d for x = f 1 2f 2 2f 3. your solution’s ready to go!. Let d= {d1,d2,d3} and f= {f1,f2,f3} be bases for a vector space v, and suppose that f1=2d1−d2 d3,f2=3d2 d3, and f3=−3d1 2d3. (a) find the change of coordinates matrix from f to d, that is d [id]f. (b) find the matrix ff [id]d (c) find [x]d for x=f1−2f2 2f3. your solution’s ready to go!.

Solved Let A A1 A2 A3 ï And D D1 D2 D3 ï Be Bases For V Chegg Let d = {d 1, d 2, d 3} and f = {f 1, f 2, f 3} be bases for a vector space v, and suppose f 1 = 2d 1 d 2 d 3 f 2 = 3d 2 d 3, and f 3 = 3d 1 2d 3. a. find the change of coordinates matrix from f to d. b. find [x] d for x = f 1 2f 2 2f 3. your solution’s ready to go!. Let d= {d1,d2,d3} and f= {f1,f2,f3} be bases for a vector space v, and suppose that f1=2d1−d2 d3,f2=3d2 d3, and f3=−3d1 2d3. (a) find the change of coordinates matrix from f to d, that is d [id]f. (b) find the matrix ff [id]d (c) find [x]d for x=f1−2f2 2f3. your solution’s ready to go!. In the book of analysis on manifolds by munkres, at page 103, question 4 b, it is asked to show that $$d 2 d 1 f (x) = d 1 d 2 f (x)$$ for all $x \in a$, where $a \subseteq \mathbb {r}^2 $ is open. For ~x = ~f1 − = (2, −1, 1), [ ~f2]d = (0, 3, 1) and [ ~f3]d = (−3, 0, 2). so by theorem 15. Enter the function you want to find the derivative of in the editor. the derivative calculator supports solving first, second ., fourth derivatives, as well as implicit differentiation and finding the zeros roots. you can also get a better visual and understanding of the function by using our graphing tool. (c) find [x] d for x = f 1 2 f 2 2 f 3. there are 3 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.

Solved Let D A 1 A 2 A 3 And D D 1 D 2 D 3 Be Chegg In the book of analysis on manifolds by munkres, at page 103, question 4 b, it is asked to show that $$d 2 d 1 f (x) = d 1 d 2 f (x)$$ for all $x \in a$, where $a \subseteq \mathbb {r}^2 $ is open. For ~x = ~f1 − = (2, −1, 1), [ ~f2]d = (0, 3, 1) and [ ~f3]d = (−3, 0, 2). so by theorem 15. Enter the function you want to find the derivative of in the editor. the derivative calculator supports solving first, second ., fourth derivatives, as well as implicit differentiation and finding the zeros roots. you can also get a better visual and understanding of the function by using our graphing tool. (c) find [x] d for x = f 1 2 f 2 2 f 3. there are 3 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly.

We were solutely delighted to have you here, ready to embark on a journey into the captivating world of Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg. Whether you were a dedicated Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg aficionado or someone taking their first steps into this exciting realm, we have crafted a space that is just for you.

Using Definite Integrals to Solve D.Es (Exam Short Cut!)

Using Definite Integrals to Solve D.Es (Exam Short Cut!)

Using Definite Integrals to Solve D.Es (Exam Short Cut!) 2.1D - Exploring the Relationship Between f, f' and f'' [AP Calculus] 32. Find (a) f+g, (b) f-g, (c) fg, and (d) f⁄g and state their domains. f(x)=√(3-x), g(x)=√(x^2-1) 1. Use the graph of f to find a number δ such that if |x-1|⋖δ then |f(x)-1|⋖0.2. Can (f*g)'=f'*g'? Learn Functions – Understand In 7 Minutes Find f(2) of the function using the Remainder Theorem! Algebra Polynomial Theory! ∫𝓒F ∙ dr = ∫∫𝓓curl(F)dA, 𝓒 = ∂𝓓 | Green's Theorem Statement and a Detailed Example How to Find the Difference Quotient || Example with f(x) = x^2 + 1 35. Find the functions (a) f°g, (b) g°f, (c) f°f, and (d) g°g and their domains. f(x)=√(x+1), g(x) Let f(x) be a function which is continuous on [ 1, 1] and differentiable on ( 1,1). f(-1) 0 and f(1… Algebra Office Hours w/ Wallace Stem - We're Live, Ask Away! Let f(x)=-3 x+1 and g(x)=x^2+2 . Find each of the following. f(2)+g(2) Finding f(0) When f(f(x))=x^2-x+1 TNB Frames (Frenet-Serret) | Calculus 3 Lesson 33 - JK Math Use Theorem 7.1 .1 to find ℒ{f(t)} f(t)=t^2+6 t-3 [HD] EECS4315 W23 - 2023-03-02 - F(phi1) implies FG(phi2): Formulation, Proofs, Disproofs, Exercises Definition of the Derivative

Conclusion

Considering all the aspects, one can see that post presents educational data about Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg. In every section, the creator manifests remarkable understanding regarding the topic. Markedly, the discussion of contributing variables stands out as a crucial point. The text comprehensively covers how these variables correlate to form a complete picture of Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg.

In addition, the text stands out in deconstructing complex concepts in an clear manner. This comprehensibility makes the content useful across different knowledge levels. The expert further bolsters the analysis by introducing applicable demonstrations and real-world applications that help contextualize the theoretical constructs.

A supplementary feature that distinguishes this content is the in-depth research of different viewpoints related to Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg. By considering these alternate approaches, the publication presents a objective picture of the matter. The comprehensiveness with which the writer handles the theme is truly commendable and sets a high standard for analogous content in this field.

Wrapping up, this article not only educates the observer about Solved Let D D 1 D 2 D 3 And F F 1 F 2 F 3 Be Chegg, but also motivates more investigation into this engaging subject. For those who are a novice or an authority, you will find useful content in this extensive content. Many thanks for your attention to this comprehensive write-up. If you would like to know more, do not hesitate to reach out by means of the comments section below. I anticipate hearing from you. For further exploration, here is a few associated publications that you will find helpful and enhancing to this exploration. May you find them engaging!