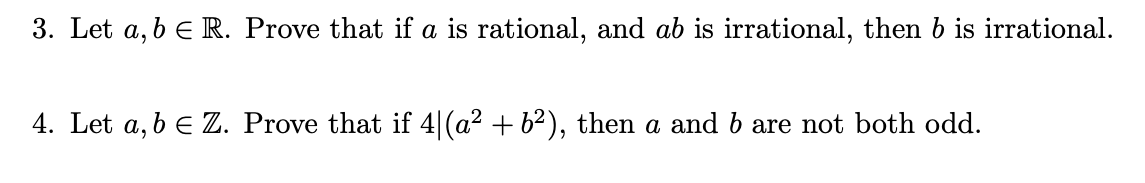
Solved 3 Let A Bв R Prove That If A Is Rational And Ab Is Chegg Let r = a b √ 2 a, b ∈ z and let r0 = a 2b b a a, b ∈ z . (a) show that r is a subring of (r, , ×), where r is the set of real numbers and and × are the usual addition and multiplication respectively. To complete the proof that ψis surjective, every element in r (a) × r (b) has the form s (a), t (b), where s,t∈ r. let r= svb tua. then, r∈ rand we have ψ(r) = ψ(s)ψ(vb) ψ(t)ψ(ua) = s (a), s (b) 1r (a), 0r (b) t (a), t (b) 0r (a), 1r (b) = s (a), 0r (b) 0r (a), t (b) = s (a), t (b) this proves the surjectivity of the ring.

Solved 10 Let A Bв Z A Prove That If A2в јb2 Then Aв јb B Chegg Define relation r on q via r= { (a,b):2a−2b∈z}. prove or disprove that r is an equivalence relation. hint: compare with exercise 11.1. use the method developed in exercises 11.6, 11.7, 11.8, to find an integer z∈ [0,11) such that z≡396 (mod11). do not actually compute 396, and explain each step of your calculation. Let z[ √ 2] = {a b √ 2 | a, b ∈ z}. (a) prove that z[ √ 2] is a subring of r. (b) find a unit in z[ √ 2] that is different than 1 or −1. there are 2 steps to solve this one. Answer: yes, r is an equivalence relation. to prove this, i need to show that r is re exive, symmetric, and transitive. re exive: let x 2z. then x2 x2 (mod 4), so xrx. symmetric: let x;y 2z so that xry. this means that x2 y2 (mod 4), which obviously means that y 2 x (mod 4) and hence that yrx, so r is symmetric. transitive: let x;y;z 2z so that. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer see answer see answer done loading.
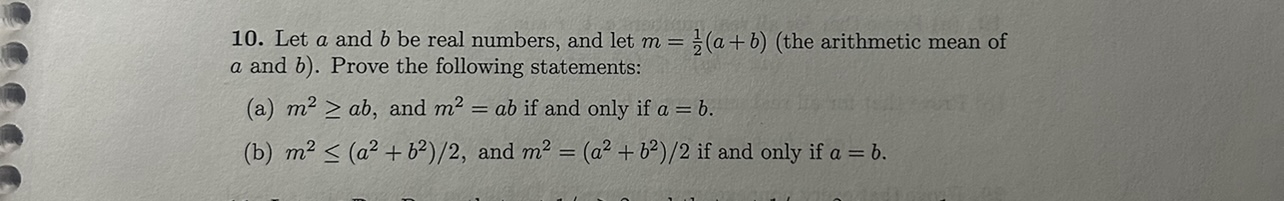
Solved Prove The Following Let A And B ï Be Real Numbers Chegg Answer: yes, r is an equivalence relation. to prove this, i need to show that r is re exive, symmetric, and transitive. re exive: let x 2z. then x2 x2 (mod 4), so xrx. symmetric: let x;y 2z so that xry. this means that x2 y2 (mod 4), which obviously means that y 2 x (mod 4) and hence that yrx, so r is symmetric. transitive: let x;y;z 2z so that. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer see answer see answer done loading. A relation $r$ is defined on $\mathbb{z}$ by $arb$ if and only if $2a 2b\equiv 0\pmod 4$. prove that $r$ is an equivalence relation. my method: let $a \in \mathbb{z}$ be given. so, for any $a \in \mathbb{z}$, we have $2a 2a = 4a$. since $4a$ is divisible by $4$, it is congruent to $0\pmod 4$. it follows that $ara$. so, $r$ is reflexive. Our √ goal is to show √ that ρ is an isomorphism. which implies that a1 = a2 and b1 = b2. hence, a1 b1 2 = a2 b2 2, which proves that ρ is one to one. onto: this is clear, given the definitions of g, √ h and ρ. √ operation preservation: let x1 = a1 b1 2, x2 = a2 b2 2 ∈ g. Let a be the set: a = {a √2b : a, b ∈ q and (a, b) ≠ (0, 0)}. we admit that √2 ∉ q . show that 0 ∉ a. (no need to prove) let r be the relation on a defined by xry ↔ x y ∈ q. (b) what is the equivalence class of 1? justify your answer. It follows that ab is an additive subgroup of r. now, let r 2r and let x be as above. then rx = r(a 1b 1 a nb n) = (ra 1)b 1 (ra n)b n which is in ab since (ra 1);(ra 2);:::;(ra n) 2a since a is an ideal. similarly xr = (a 1b 1 a nb n)r = a 1(b 1r) a n(b nr) which is in ab since (b 1r);(b 2r);:::;(b nr) 2b since b is an ideal. thus.

Solved Activity 1 6e Prove That в A B в Aв B Let A Bв Z Chegg A relation $r$ is defined on $\mathbb{z}$ by $arb$ if and only if $2a 2b\equiv 0\pmod 4$. prove that $r$ is an equivalence relation. my method: let $a \in \mathbb{z}$ be given. so, for any $a \in \mathbb{z}$, we have $2a 2a = 4a$. since $4a$ is divisible by $4$, it is congruent to $0\pmod 4$. it follows that $ara$. so, $r$ is reflexive. Our √ goal is to show √ that ρ is an isomorphism. which implies that a1 = a2 and b1 = b2. hence, a1 b1 2 = a2 b2 2, which proves that ρ is one to one. onto: this is clear, given the definitions of g, √ h and ρ. √ operation preservation: let x1 = a1 b1 2, x2 = a2 b2 2 ∈ g. Let a be the set: a = {a √2b : a, b ∈ q and (a, b) ≠ (0, 0)}. we admit that √2 ∉ q . show that 0 ∉ a. (no need to prove) let r be the relation on a defined by xry ↔ x y ∈ q. (b) what is the equivalence class of 1? justify your answer. It follows that ab is an additive subgroup of r. now, let r 2r and let x be as above. then rx = r(a 1b 1 a nb n) = (ra 1)b 1 (ra n)b n which is in ab since (ra 1);(ra 2);:::;(ra n) 2a since a is an ideal. similarly xr = (a 1b 1 a nb n)r = a 1(b 1r) a n(b nr) which is in ab since (b 1r);(b 2r);:::;(b nr) 2b since b is an ideal. thus.

6 Let R Z 2 A Prove That A B2в Rг If And Only If Chegg Let a be the set: a = {a √2b : a, b ∈ q and (a, b) ≠ (0, 0)}. we admit that √2 ∉ q . show that 0 ∉ a. (no need to prove) let r be the relation on a defined by xry ↔ x y ∈ q. (b) what is the equivalence class of 1? justify your answer. It follows that ab is an additive subgroup of r. now, let r 2r and let x be as above. then rx = r(a 1b 1 a nb n) = (ra 1)b 1 (ra n)b n which is in ab since (ra 1);(ra 2);:::;(ra n) 2a since a is an ideal. similarly xr = (a 1b 1 a nb n)r = a 1(b 1r) a n(b nr) which is in ab since (b 1r);(b 2r);:::;(b nr) 2b since b is an ideal. thus.
