Solved Let S 1 2 3 4 5 6 7 8 Part 1 Find %d0%b2 %d1%98p S %d0%b2 %d1%98 I E Chegg

Solved Let S 1 2 3 4 5 6 7 The Relation R 1 Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: let s= {1,2,3,4,5,6,7,8} part 1 find ∣p (s)∣ i.e., find the total number of subsets of s. don't forget \ {\} is a subset of every set. part 2 how many subsets of s have 6 elements?. To find the subsets that have {2,3,5} as a subset, we consider the three elements as a single unit. since we have 2 choices for each element (either include it or exclude it), the number of subsets with {2,3,5} as a subset is 2³ = 8.

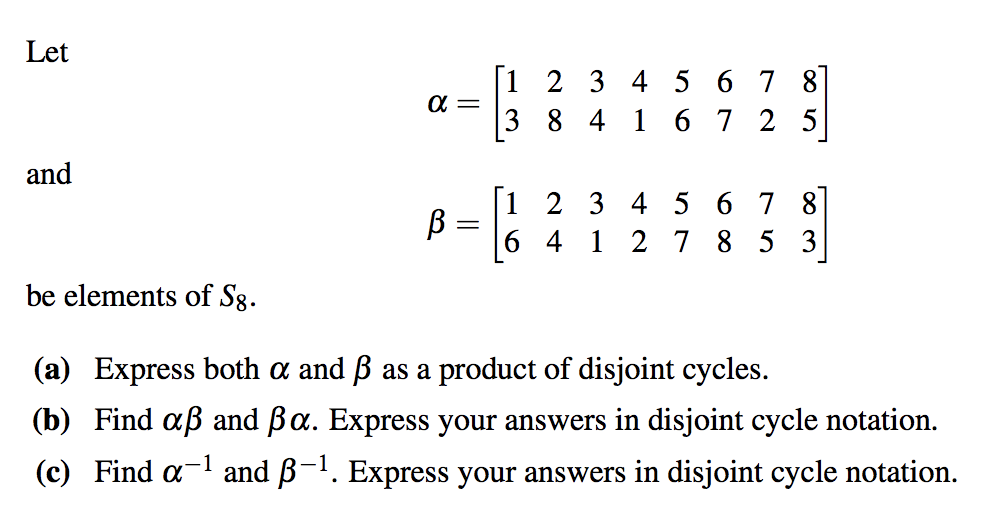
Solved Let 顛i 2 3 4 5 6 7 8 A 3 8 4 1 6 7 2 5 And B 1 2 Chegg Five families of numbers appear : $ (1,2,4,8)$, $ (3,6)$, $ (5,10)$, $ (7)$ and $ (9)$ (two numbers which can or cannot be in $a$ without any consequence on the property). To find the order of σ, we need to consider the cycles that make up σ. the permutation σ is given as a product of two cycles: (1 2 3 4) and (5 6 7 4 8). however, there is a mistake in the permutation as written: the element 4 appears in both cycles, which is not possible in a permutation. To solve the problem, we need to find the values of the function g(n) for n= 1,2,3,4,5 and then compute g(10)⋅(g(1) g(2) g(3) g(4) g(5)). step 1: define the function f(n). To find the number of subsets of s that contain an even number of elements, we note that the total number of subsets of s is 512, as calculated in part a. half of these subsets will contain an even number of elements, and half will contain an odd number of elements.

Solved Let S 1 2 3 4 5 And Let T 3 4 5 6 7 Chegg To solve the problem, we need to find the values of the function g(n) for n= 1,2,3,4,5 and then compute g(10)⋅(g(1) g(2) g(3) g(4) g(5)). step 1: define the function f(n). To find the number of subsets of s that contain an even number of elements, we note that the total number of subsets of s is 512, as calculated in part a. half of these subsets will contain an even number of elements, and half will contain an odd number of elements. Let a = { {1, 2, 3}, {4, 5}, {6, 7, 8}}. determine which of the following is true or false: (i) 1 ∈ a (ii) {1, 2, 3} ⊂ a (iii) {6, 7, 8} ∈ a (iv) {4, 5} ⊂ a (v) ϕ ∈ a (vi) ϕ ⊂ a. Let s = {1,2,3,4,5,6,7} . then the number of possible function f: s →s such that f (m⋅n)= f (m)⋅f (n) for every m,n∈s and m⋅n∈s is equal to . not the question you're searching for? was this solution helpful? learn from their 1 to 1 discussion with filo tutors.

Solved Let A 1 2 3 4 5 6 B 3 4 5 7 8 9 Chegg Let a = { {1, 2, 3}, {4, 5}, {6, 7, 8}}. determine which of the following is true or false: (i) 1 ∈ a (ii) {1, 2, 3} ⊂ a (iii) {6, 7, 8} ∈ a (iv) {4, 5} ⊂ a (v) ϕ ∈ a (vi) ϕ ⊂ a. Let s = {1,2,3,4,5,6,7} . then the number of possible function f: s →s such that f (m⋅n)= f (m)⋅f (n) for every m,n∈s and m⋅n∈s is equal to . not the question you're searching for? was this solution helpful? learn from their 1 to 1 discussion with filo tutors.

Solved 3 Let A 1 2 3 4 5 6 And 1 2 3 4 5 6 P1 Chegg

Solved Let A 1 2 3 4 5 6 7 8 Let B 2 3 5 Chegg