
Solved Problem 5 Recall That The Standard Basis Of R2 Is E Chegg Given, s = {e 1 = (1, 0), e 2 = (0, 1)} is standard basis of r 2. and b = {v 1, v 2} is a basis obtained by reflection of vectors of s. along the lin. Let $a$ be the reflection of the plane $\mathbb r^2$ in the line $y= x$. find the matrix of $a$ in the standard basis $s=\{e 1,e 2\}$.

Solved Recall That The Standard Basis Of R2 Is E E1 E2 Chegg Geometrically, a should be the length of the projection of e 2 onto the line through c 1 and b should be the projection of e 2 on the line through c 2 so it looks like a = b. this is because c 1 and c 2 are perpendicular. let’s check. by theorem (1) we have [e 2] c = p c b [e 2] b = p c b 0 1 = 2nd column of p c b:. Let s = {e₁, e₂} be the standard basis for r², and let b = {v₁, v₂} be the basis that results when the vectors in s are reflected about the line that makes an angle θ with the positive x axis. (a) find the transition matrix. p {b→s}. p b →s. p = p {b→s}. p = p b →s. p^t = p {s→b}. p t = p s →b. Let s = {e1, e2} be the standard basis for r 2, and let b = {v1, v2} be the basis that results when the vectors in s are. reflected about the line that makes an angle θ with the positive x axis. (a) find the transition matrix pb → s . (b) let p = pb → s and show that pt = ps → b. Let s = {e 1, e 2} be the standard basis for r^2, and let b = {v 1, v 2} be the basis that results when the vectors in s are reflected about the line y = x. (a) find the transition matrix p b rightarrow s. p b rightarrow s =.
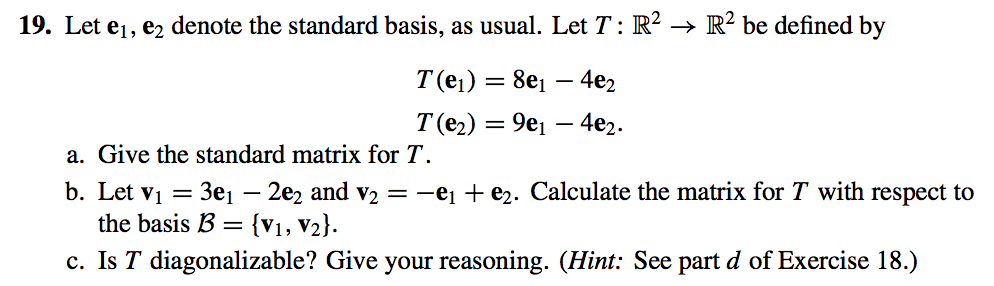
Solved Let E 1 E 2 Denote The Standard Basis As Usual Let Chegg Let s = {e1, e2} be the standard basis for r 2, and let b = {v1, v2} be the basis that results when the vectors in s are. reflected about the line that makes an angle θ with the positive x axis. (a) find the transition matrix pb → s . (b) let p = pb → s and show that pt = ps → b. Let s = {e 1, e 2} be the standard basis for r^2, and let b = {v 1, v 2} be the basis that results when the vectors in s are reflected about the line y = x. (a) find the transition matrix p b rightarrow s. p b rightarrow s =. Compute the change of basis matrices p and p . apply the second change of basis formula from theorem 2 (pg 13). in the formulas) amd = ff1; f2g. it is easy to compute p for any basis 2 rn. then you compute. by inverting p . so \writing in terms of ". 1p 1p ! step 2 apply the second change of basis formula. 1p 1p ! a b !. So in this case let's consider the following basis. which is as corresponds to the standard basis for our two. and then we're going to define the basis b composed by p one and p two. Let e 1, e 2 denote the standard basis, as usual. let t: r^2rightarrow r^2 be defined by give the standard matrix for t. let v 1 = 3e 1 2e 2 and v 2 = e 1 e 2. calculate the matrix for t with respect to the basis b = {v 1, v 2}. is t diagonalizable? give your reasoning. (see part d of exercise 18.). Let s= {e1,e2} be the standard basis for the vector space r2, and let b= {v1,v2} be the basis that results when the vectors in s are reflected about the line that makes an angle θ with the positive x axis. a. find the transition matrix pb→s. b. let p=pb→s and show that pt=ps→b. your solution’s ready to go!.
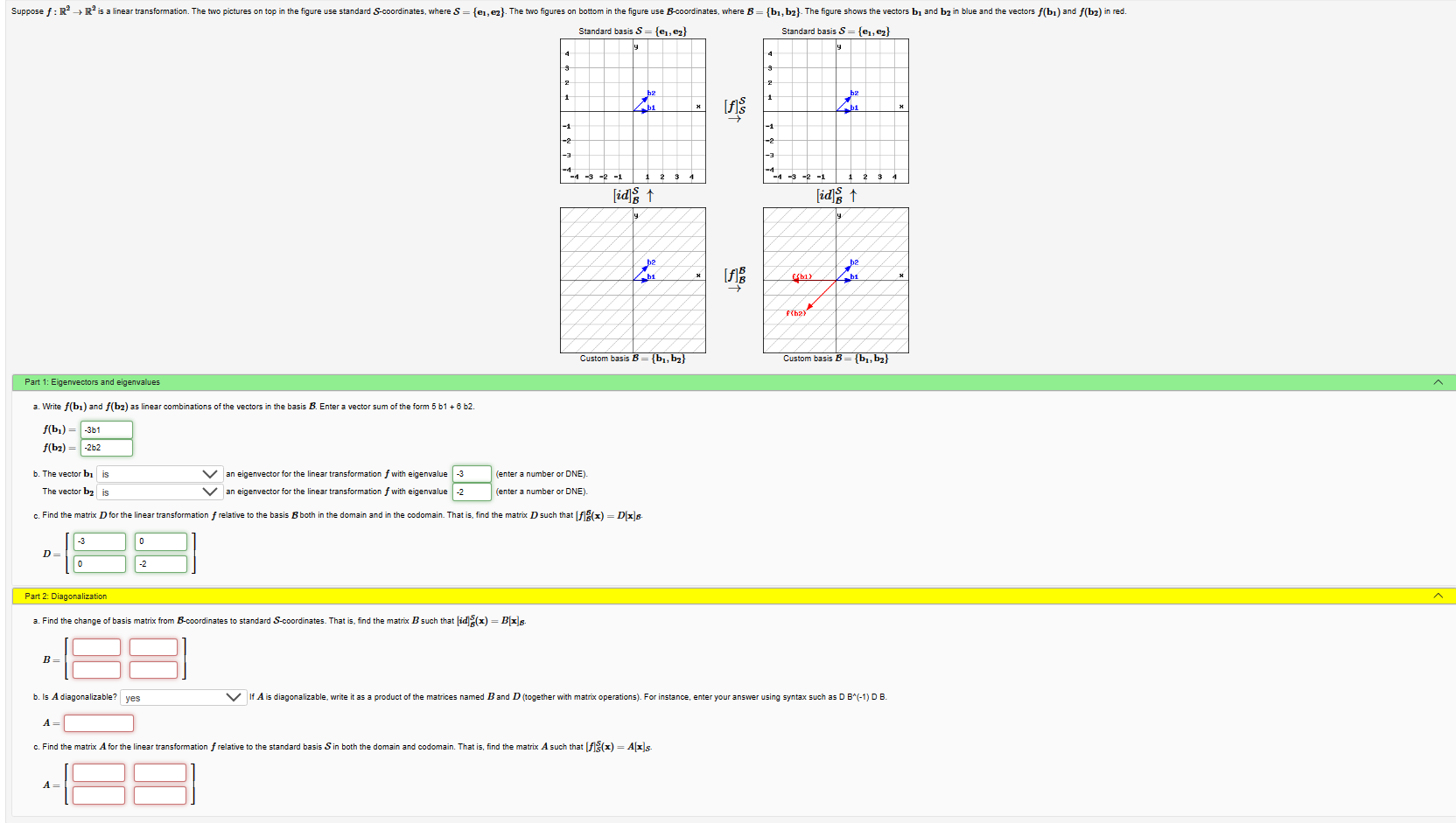
Solved Standard Basis S E1 E2 Standard Basis Chegg Compute the change of basis matrices p and p . apply the second change of basis formula from theorem 2 (pg 13). in the formulas) amd = ff1; f2g. it is easy to compute p for any basis 2 rn. then you compute. by inverting p . so \writing in terms of ". 1p 1p ! step 2 apply the second change of basis formula. 1p 1p ! a b !. So in this case let's consider the following basis. which is as corresponds to the standard basis for our two. and then we're going to define the basis b composed by p one and p two. Let e 1, e 2 denote the standard basis, as usual. let t: r^2rightarrow r^2 be defined by give the standard matrix for t. let v 1 = 3e 1 2e 2 and v 2 = e 1 e 2. calculate the matrix for t with respect to the basis b = {v 1, v 2}. is t diagonalizable? give your reasoning. (see part d of exercise 18.). Let s= {e1,e2} be the standard basis for the vector space r2, and let b= {v1,v2} be the basis that results when the vectors in s are reflected about the line that makes an angle θ with the positive x axis. a. find the transition matrix pb→s. b. let p=pb→s and show that pt=ps→b. your solution’s ready to go!.

Solved Let S E 1 E 2 Be The Standard Basis For R 2 And Chegg Let e 1, e 2 denote the standard basis, as usual. let t: r^2rightarrow r^2 be defined by give the standard matrix for t. let v 1 = 3e 1 2e 2 and v 2 = e 1 e 2. calculate the matrix for t with respect to the basis b = {v 1, v 2}. is t diagonalizable? give your reasoning. (see part d of exercise 18.). Let s= {e1,e2} be the standard basis for the vector space r2, and let b= {v1,v2} be the basis that results when the vectors in s are reflected about the line that makes an angle θ with the positive x axis. a. find the transition matrix pb→s. b. let p=pb→s and show that pt=ps→b. your solution’s ready to go!.
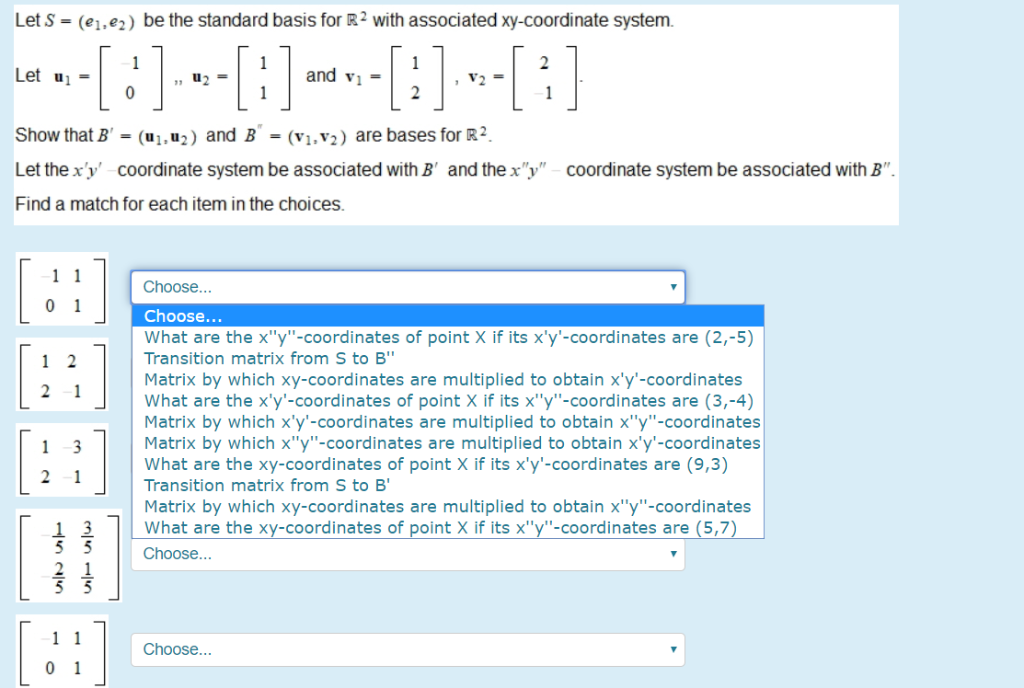
Solved Let S E E2 Be The Standard Basis For R2 With Chegg
