
Solved 1 Pt Let Denote The Standard Basis For R2 Let β Chegg Let s = (e1, e2) be the standard ordered basis of r2 and b = (b1, b2) be another ordered basis. let a = be the matrix that transforms the components of a vector x r2 from the basis s into the basis b, that is, xb = axs. Let (e 1, e 2) denote the standard ordered basis for r 2, for each θ i n r, let r θ: r 2 → r 2 be the linear operator r θ ( e 1 ) = ( c o s ( θ ) , s i n ( θ ) ) and r θ ( e 2 ) = ( s i n ( θ ) , c o s ( θ.

Solved 5 A Let E Be The Standard Ordered Basis For Rand Chegg X = [x 1, x 2] t = x 1 e 1 x 2 e 2 where {e 1, e 2} is standard ordered basis. reflection theorem: let t : r 2 → r 2 be a linear transformation given by reflecting vectors over the line x 2 = m x 1 . If x 1 and x 2 are the components of a vector x with respect to a standard basis, this means. x = [x 1, x 2] t = x 1 e 1 x 2 e 2 where {e 1, e 2} is standard ordered basis. reflection theorem: let t : r 2 → r 2 be a linear transformation given by reflecting vectors over the line x 2 = m x 1. then the matrix of t is given by. Step by step solution: step 1. to determine if it is possible to have such a linear transformation t, we will look at what happens to a general vector, say (a,b) in r^2 under t. step 2. using the linearity of t, we have t(a,b) = at(e1) bt(e2). step 3. from the given condition, we know that t(e1) lies in r and t(e2) lies in r^2. step 4. Question 3.4.6: let b = {e1, e2} be the standard ordered basis for r² , b′ b and let v=\begin {bmatrix} 3 \\ 4\end {bmatrix} . a. find the transition matrix from b to b′. b. find \left [v\right] {b^ {′}} . c. write the vector v as a linear combination of e {1} and e {2} and also as a linear combination of v^ {′} {1} and v^ {′} {2}. d.

Solved Let S E1 E2 Be The Standard Ordered Basis Of R2 Chegg Step by step solution: step 1. to determine if it is possible to have such a linear transformation t, we will look at what happens to a general vector, say (a,b) in r^2 under t. step 2. using the linearity of t, we have t(a,b) = at(e1) bt(e2). step 3. from the given condition, we know that t(e1) lies in r and t(e2) lies in r^2. step 4. Question 3.4.6: let b = {e1, e2} be the standard ordered basis for r² , b′ b and let v=\begin {bmatrix} 3 \\ 4\end {bmatrix} . a. find the transition matrix from b to b′. b. find \left [v\right] {b^ {′}} . c. write the vector v as a linear combination of e {1} and e {2} and also as a linear combination of v^ {′} {1} and v^ {′} {2}. d. Let t: r2 → r2 be defined by t (e1) = 8e1 − 4e2 t (e2) = 9e1 − 4e2 a. give the standard matrix for t . b. let v1 = 3e1 − 2e2 and v2 = −e1 e2 . calculate the matrix for t with respect to the basis $\mathcal {b}=\left\ {\mathbf {v} {1}, \mathbf {v} {2}\right\}.c.i s t diagonalizable?giveyourreasoning.(h int: s eepart d$ of exercise 18.). Let s be the standard basis for r3, and let b = {v1, v2, v3) be the basis in which v1 = (1, 2, 1), v2 = (2, 5, 0) , and v3 = (3, 3, 8). (a) find the transition matrix pb→s by inspection. (b) find the transition matrix ps→b. (c) confirm that pb→s and ps→b are inverses of one another. (d) let w = (5, 3, 1). Let t: r^5 > r^5 be the linear transformation whose representing matrix with respect to the standard basis for r^5 is given by [t] = [5 1] [0 2] compute basis for the ker (t). b) compute basis for the im (t). define, if possible, a linear transformation s: r^5 > r' such that t o s is onto. if not possible, explain why. If b ={v1,v2, ,vn} is an ordered basis for v and v is a vector in v, then the scalars c 1 ,c 2 , ,c n in the unique n tuple (c 1 ,c 2 , ,c n ) such that v = c 1 v 1 c 2 v 2 ··· c n v n.

7 Let S Be An Ordered Basis For R 3 Suppose T Is Chegg Let t: r2 → r2 be defined by t (e1) = 8e1 − 4e2 t (e2) = 9e1 − 4e2 a. give the standard matrix for t . b. let v1 = 3e1 − 2e2 and v2 = −e1 e2 . calculate the matrix for t with respect to the basis $\mathcal {b}=\left\ {\mathbf {v} {1}, \mathbf {v} {2}\right\}.c.i s t diagonalizable?giveyourreasoning.(h int: s eepart d$ of exercise 18.). Let s be the standard basis for r3, and let b = {v1, v2, v3) be the basis in which v1 = (1, 2, 1), v2 = (2, 5, 0) , and v3 = (3, 3, 8). (a) find the transition matrix pb→s by inspection. (b) find the transition matrix ps→b. (c) confirm that pb→s and ps→b are inverses of one another. (d) let w = (5, 3, 1). Let t: r^5 > r^5 be the linear transformation whose representing matrix with respect to the standard basis for r^5 is given by [t] = [5 1] [0 2] compute basis for the ker (t). b) compute basis for the im (t). define, if possible, a linear transformation s: r^5 > r' such that t o s is onto. if not possible, explain why. If b ={v1,v2, ,vn} is an ordered basis for v and v is a vector in v, then the scalars c 1 ,c 2 , ,c n in the unique n tuple (c 1 ,c 2 , ,c n ) such that v = c 1 v 1 c 2 v 2 ··· c n v n.
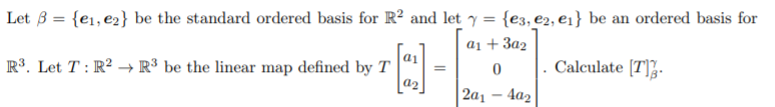
Solved Let β Ei E Be The Standard Ordered Basis For R2 Chegg Let t: r^5 > r^5 be the linear transformation whose representing matrix with respect to the standard basis for r^5 is given by [t] = [5 1] [0 2] compute basis for the ker (t). b) compute basis for the im (t). define, if possible, a linear transformation s: r^5 > r' such that t o s is onto. if not possible, explain why. If b ={v1,v2, ,vn} is an ordered basis for v and v is a vector in v, then the scalars c 1 ,c 2 , ,c n in the unique n tuple (c 1 ,c 2 , ,c n ) such that v = c 1 v 1 c 2 v 2 ··· c n v n.

Solved Let S Be The Standard Ordered Basis Of R2 2 That Is Chegg
