
Solved Let U 2 1 4 3 And V 1 1 1 0 Find U V A Chegg There are 2 steps to solve this one. give let u = (1, 0, 2) and v = (3, 2, 4). compute 2u v. (a) (4, 2, 2) (b) (5, 2, 0) (c) (6, 5, 0) (d) (7, 2, 2) what is the terminal point of a vector with initial point a ( 1, 0) that is equivalent to u = (3, 4)? (a) (3, 3) (b) (4, 4) (c) (3, 4) (d) (2, 4) let ||v|| = 3. The two equations u−w = 3 and v 2w = −1 specify a line of solutions; to find one solution, just let w = 0 and solve for u and v. this yields the solution (u,v,w) = (3,−1,0).
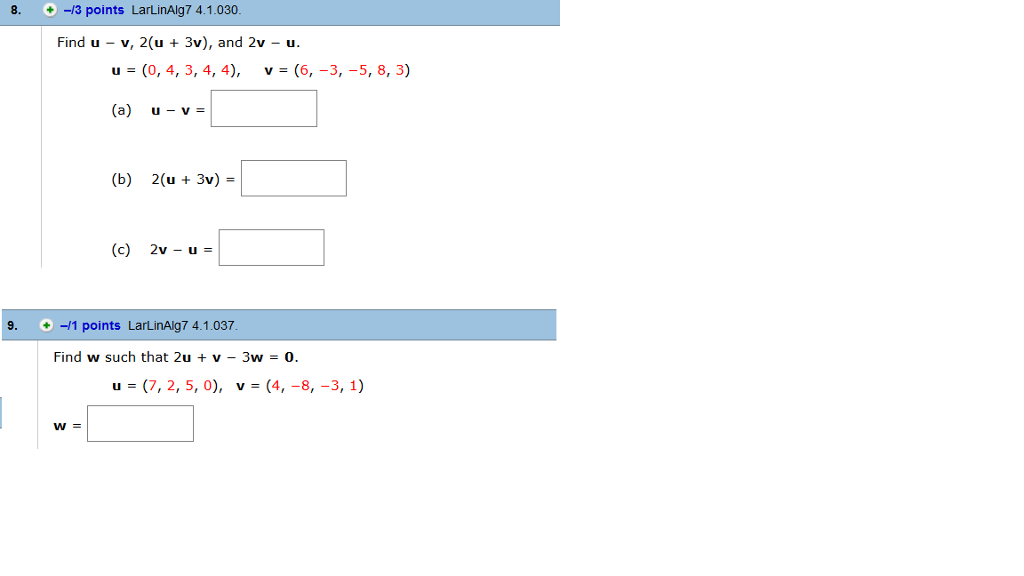
Solved Find U V 2 U 3v And 2v U U 0 4 3 4 Chegg V) = x(u) vv(u). let x(u0, . 0) be a point of s. then, since s is developable, the tangent plane tx(u0,v0)s is tangent to d all along the line v 7�. x(u0, v0) vv(u0). hence, the normal n to s is constant along this line; since this is true for all choices of u0 and v0, we see that n. ≡ 0 on all of s. in particula. Our expert help has broken down your problem into an easy to learn solution you can count on. question: let u = 2 and v = a 3 b 4 c compute utv, vtu, uvt, and vut. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Multiply the x component and the y component of vector u by 2 to get the vector 2u. multiply both components of vector v by 3 to get vector 3v. now subtract the x and y compnents of 3v from those of 2u to get the components of 2u 3v. add the x and y components of u and v separately to give the components of u v. i hope this helps. Question: let u =(1, 0, 2) and v = (3, 2, 4). compute 2u v. (4, 2, 2) (5, 2, 0) (6, 5, 0) (7, 2, 2) what is the terminal point of a vector with initial point a( 1, 0)that is equivalent to u = (3, 4)?.
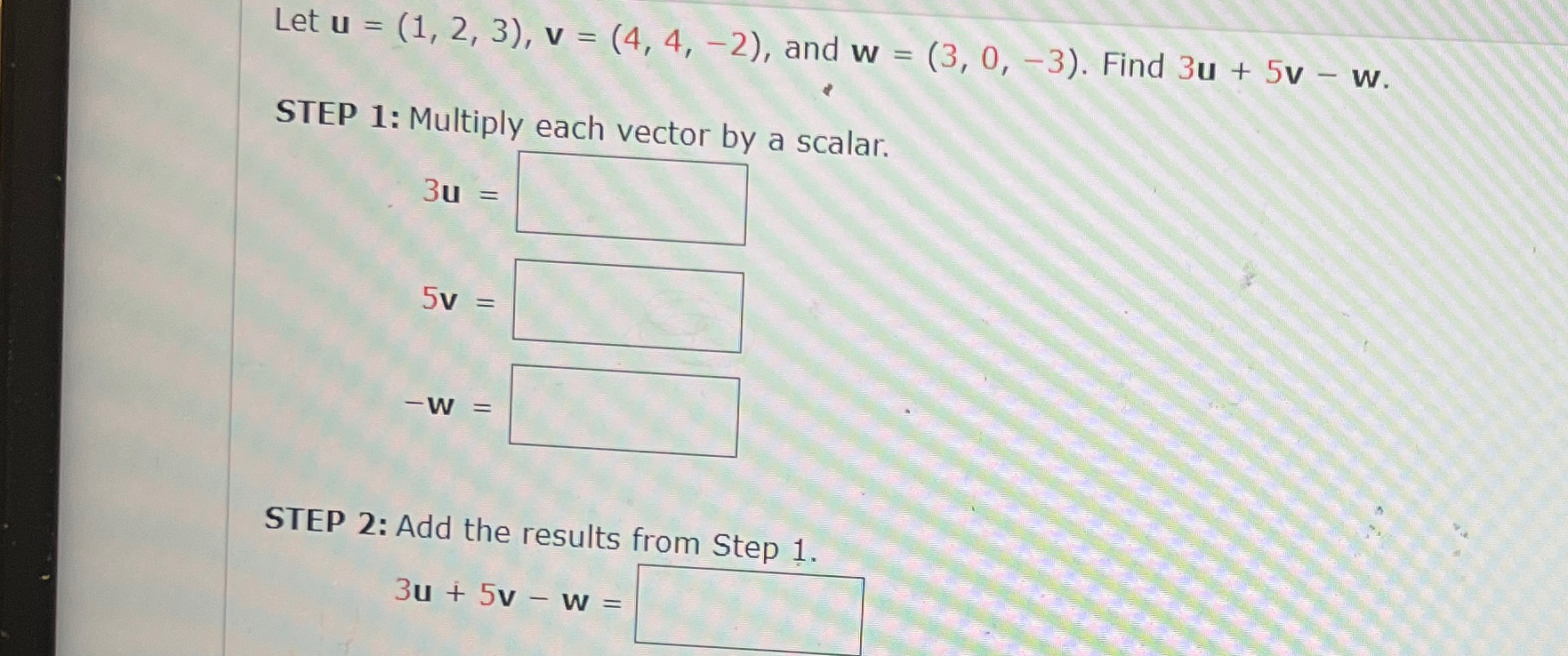
Solved Let U 1 2 3 V 4 4 2 ï And W 3 0 3 ï Find Chegg Multiply the x component and the y component of vector u by 2 to get the vector 2u. multiply both components of vector v by 3 to get vector 3v. now subtract the x and y compnents of 3v from those of 2u to get the components of 2u 3v. add the x and y components of u and v separately to give the components of u v. i hope this helps. Question: let u =(1, 0, 2) and v = (3, 2, 4). compute 2u v. (4, 2, 2) (5, 2, 0) (6, 5, 0) (7, 2, 2) what is the terminal point of a vector with initial point a( 1, 0)that is equivalent to u = (3, 4)?. Noting that $u$ and $v$ are both unit vectors, i.e. $\|u\|=\|v\|=1$, we can then state that: $\begin{eqnarray}\|u v\|^2 & = & (u v) \cdot (u v) \\ & = & u \cdot u v \cdot v 2(u \cdot v) \\ & = & \|u\|^2 \|v\|^2 2(u \cdot v) \\ \left (\frac{3}{2} \right )^2 & = & 1 1 2(u \cdot v) \\ \therefore u \cdot v & = & \frac{1}{8}\end{eqnarray}$. Projection of v = (1, 1, 2) onto u = (−2, 3, 1). solution. we have |u| = p (−2)2 32 12 = √ 14 and u |u| = 1 √ 14 (−2, 3, 1). the scalar projection of v onto u is c = v · u |u| = 1 √ 14 (−2 3 2) = 3 √ 14. the vector projection of v onto u is p = c u |u| = 3 14 (−2, 3, 1) = − 3 7, 9 14, 3 14 . 6. Linear combination of u and v. 15. let o(0,0), a(2,2), b(4,4), c(2,−1), d(4,1), e(6,3), f(2,−4), g(6,0), h(8,2) be the indicated points in the xy plane. let u = −→ oa be the vector pictured by the arrow from o to a and v = −−→ oc the vector pictured by the arrow from o to c. find u and v. then express the vector −−→. In this case, the vectors a = (1, 1) and b = (1, 0) represent the functions f(x) and g(x), respectively. by calculating the dot product a · b, we obtain a value of 1. to find cosθ, we divide the dot product by the product of the magnitudes of a and b. since the magnitudes of both a and b are √2, we have cosθ = 1 (√2 * √2) = 1 2.
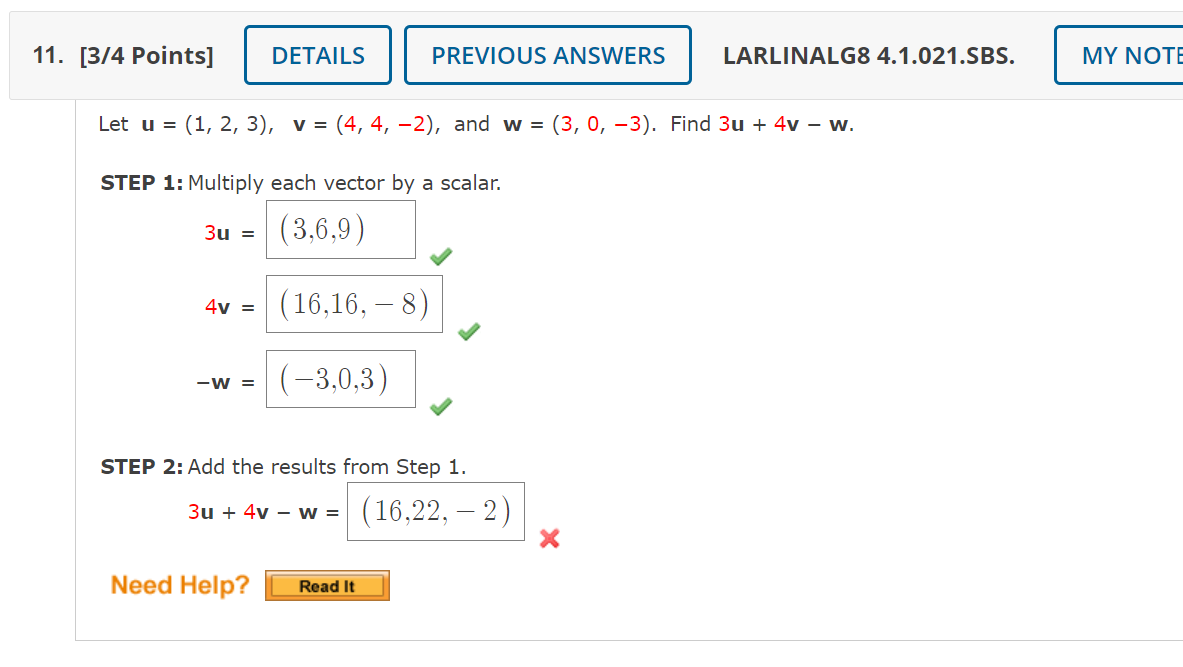
Solved Let U 1 2 3 V 4 4 2 And W 3 0 3 Find Chegg Noting that $u$ and $v$ are both unit vectors, i.e. $\|u\|=\|v\|=1$, we can then state that: $\begin{eqnarray}\|u v\|^2 & = & (u v) \cdot (u v) \\ & = & u \cdot u v \cdot v 2(u \cdot v) \\ & = & \|u\|^2 \|v\|^2 2(u \cdot v) \\ \left (\frac{3}{2} \right )^2 & = & 1 1 2(u \cdot v) \\ \therefore u \cdot v & = & \frac{1}{8}\end{eqnarray}$. Projection of v = (1, 1, 2) onto u = (−2, 3, 1). solution. we have |u| = p (−2)2 32 12 = √ 14 and u |u| = 1 √ 14 (−2, 3, 1). the scalar projection of v onto u is c = v · u |u| = 1 √ 14 (−2 3 2) = 3 √ 14. the vector projection of v onto u is p = c u |u| = 3 14 (−2, 3, 1) = − 3 7, 9 14, 3 14 . 6. Linear combination of u and v. 15. let o(0,0), a(2,2), b(4,4), c(2,−1), d(4,1), e(6,3), f(2,−4), g(6,0), h(8,2) be the indicated points in the xy plane. let u = −→ oa be the vector pictured by the arrow from o to a and v = −−→ oc the vector pictured by the arrow from o to c. find u and v. then express the vector −−→. In this case, the vectors a = (1, 1) and b = (1, 0) represent the functions f(x) and g(x), respectively. by calculating the dot product a · b, we obtain a value of 1. to find cosθ, we divide the dot product by the product of the magnitudes of a and b. since the magnitudes of both a and b are √2, we have cosθ = 1 (√2 * √2) = 1 2.

Solved Let U 1 2 3 V 4 4 2 And W 3 0 3 Find Chegg Linear combination of u and v. 15. let o(0,0), a(2,2), b(4,4), c(2,−1), d(4,1), e(6,3), f(2,−4), g(6,0), h(8,2) be the indicated points in the xy plane. let u = −→ oa be the vector pictured by the arrow from o to a and v = −−→ oc the vector pictured by the arrow from o to c. find u and v. then express the vector −−→. In this case, the vectors a = (1, 1) and b = (1, 0) represent the functions f(x) and g(x), respectively. by calculating the dot product a · b, we obtain a value of 1. to find cosθ, we divide the dot product by the product of the magnitudes of a and b. since the magnitudes of both a and b are √2, we have cosθ = 1 (√2 * √2) = 1 2.
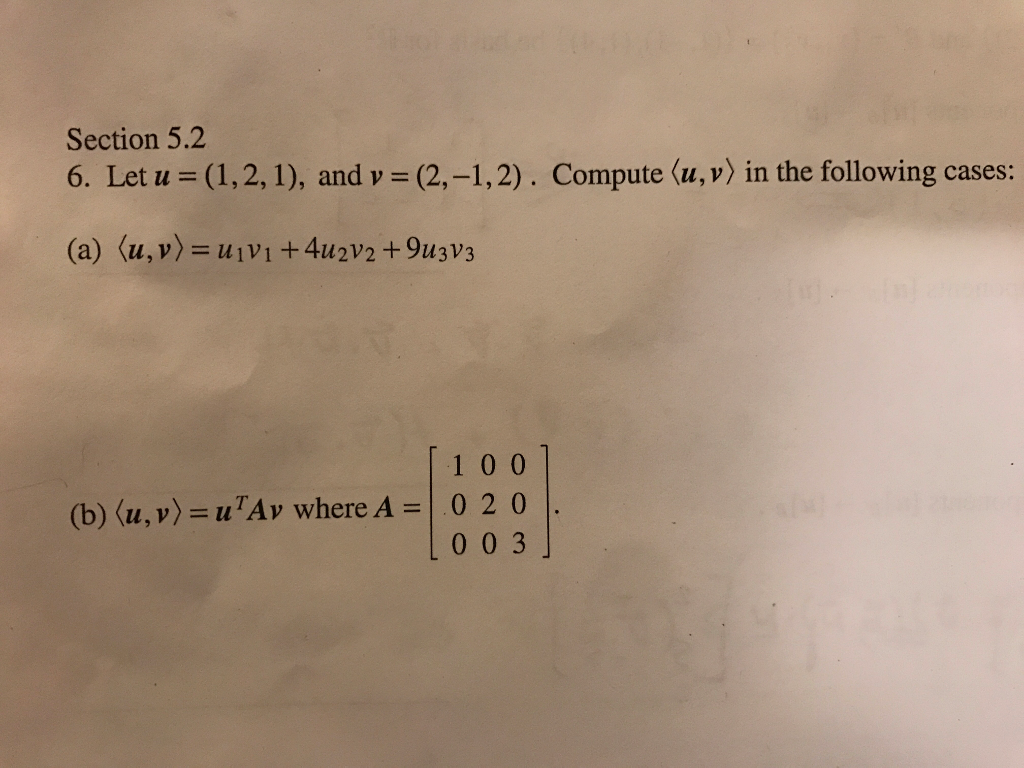
Solved Let U 1 2 1 And V 2 1 2 Compute U V Chegg
