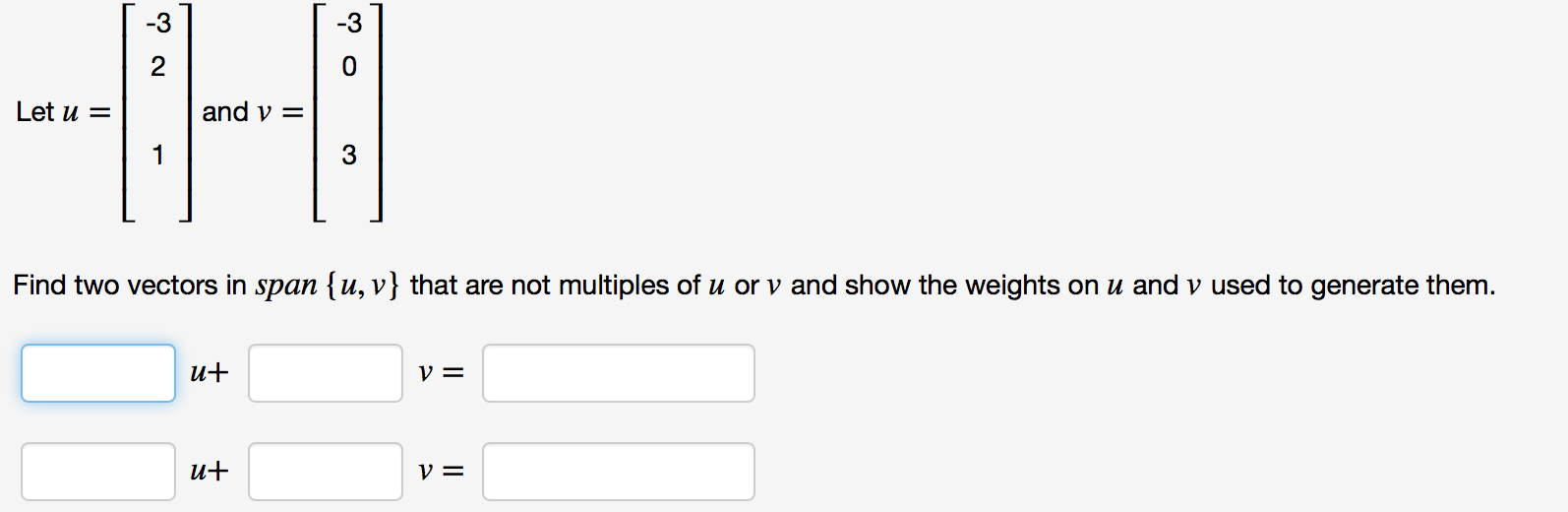
Solved Let U 3 2 1 And V 3 0 3 Find Two Vectors Chegg Let u = [ 3 2 1] and v = [ 3 0 3] find two vectors in span {u, v} that are not multiples of u or v and show the weights on u and v used to generate them. u v = u v =. Let u=(3, 2,1) and v=( 1,1,1) be two vectors in r3.(a) calculate the dot product u*v. what does it say about the angle between u and v ?(b) compute the lengths ||u|| and ||v|| of the vectors.(c) compute cosθ, where θ(0≤θ≤π) is the angle between u and v.(d) find the unit vector hat(u) in the.

Solved Let U 03 ï And V 2 1 A ï Draw The Vectors U ï And Chegg Question: exercise set 3.5in exercises 1 2, let u=(3,2, 1),v=(0,2, 3), and w=(2,6,7). compute the indicated vectors.2. (a) u×v(b) (u×v)(c) u×(v w)(d) w*(w×v)(c) w×w(f) in exercises 13 14, find the area of the triangle with the given vertices.a(1,1),b(2,2),c(3, 3)in exercises 25 26, suppose that u*(v×w)=3. find26. (a. In this tutorial, we'll learn how to calculate the magnitude, dot and cross product and angle between two vectors in the coordinate plane and space. the magnitude is the length of a vector. the formula for the magnitude of a vector v= (v 1, v 2) is: example 01: find the magnitude of the vector v= (4, 2). Let u = [ 3 2 3] v = [ 1 1 3] a. find ||u|| b. find the distance between u and v. c. find a unit vector in the direction of u. d. find the cosine of the angle between the two vectors. are the vectors orthogonal? explain. e. find a vector in the opposite direction of v with length 3. f. find a scalar c, so that [c 3] is orthogonal to [ 1 2]. Let u →, v → and w → be vectors in ℝ 2 or ℝ 3 and let c be a scalar. the last statement of the theorem makes a handy connection between the magnitude of a vector and the dot product with itself. our definition and theorem give properties of the dot product, but we are still likely wondering “what does the dot product mean?”.

Solved 1 A Let U 3 2 1 V 0 2 3 V 2 6 7 Chegg Let u = [ 3 2 3] v = [ 1 1 3] a. find ||u|| b. find the distance between u and v. c. find a unit vector in the direction of u. d. find the cosine of the angle between the two vectors. are the vectors orthogonal? explain. e. find a vector in the opposite direction of v with length 3. f. find a scalar c, so that [c 3] is orthogonal to [ 1 2]. Let u →, v → and w → be vectors in ℝ 2 or ℝ 3 and let c be a scalar. the last statement of the theorem makes a handy connection between the magnitude of a vector and the dot product with itself. our definition and theorem give properties of the dot product, but we are still likely wondering “what does the dot product mean?”. Check if it is well defined: the term v 3 involves dividing a scalar (3) by a vector (v). division by a vector is not a defined operation in r 3 . final answer:. Theorem 4.1.2 let u,v,w be three vectors in the plane and let c,d be two scalar. 1. u v is a vector in the plane closure under addition 2. u v = v u commutative property of addition 3. (u v) w = u (v w) associate property of addition 4. (u 0) = u additive identity 5. u (−1)u = 0 additive inverse. (a) f(0;1; 3);(0; 2;6);(4;2; 6)g solution: denote u = (0;1; 3), v = (0; 2;6), w = (4;2; 6). note that v = 2u and u;w are linearly independent (not parallel to each other), thus the set of all linear combination of u;v;w is two dimensional, i.e. a plane. (b) f(2;1;0);(1;1;1);(4;3;2)g solution: denote u = (2;1;0), v = (1;1;1), w = (4;3;2). Our expert help has broken down your problem into an easy to learn solution you can count on. question: (4) (3 marks) let u = [3, 2, 1] and v= [1, 3, 2] be two vectors in z. find all scalars b in z5 such that (u bv) • (bu v) = 1. (5) (3 marks) let v = [2,0,−1] and w = [0, 2,3].

Solved Let U 3 2 5 V 0 1 2 W 2 6 3 Are Vectors Chegg Check if it is well defined: the term v 3 involves dividing a scalar (3) by a vector (v). division by a vector is not a defined operation in r 3 . final answer:. Theorem 4.1.2 let u,v,w be three vectors in the plane and let c,d be two scalar. 1. u v is a vector in the plane closure under addition 2. u v = v u commutative property of addition 3. (u v) w = u (v w) associate property of addition 4. (u 0) = u additive identity 5. u (−1)u = 0 additive inverse. (a) f(0;1; 3);(0; 2;6);(4;2; 6)g solution: denote u = (0;1; 3), v = (0; 2;6), w = (4;2; 6). note that v = 2u and u;w are linearly independent (not parallel to each other), thus the set of all linear combination of u;v;w is two dimensional, i.e. a plane. (b) f(2;1;0);(1;1;1);(4;3;2)g solution: denote u = (2;1;0), v = (1;1;1), w = (4;3;2). Our expert help has broken down your problem into an easy to learn solution you can count on. question: (4) (3 marks) let u = [3, 2, 1] and v= [1, 3, 2] be two vectors in z. find all scalars b in z5 such that (u bv) • (bu v) = 1. (5) (3 marks) let v = [2,0,−1] and w = [0, 2,3].

Solved 3 Let U 2 1 3 2 V 0 4 2 2 Find Two Chegg (a) f(0;1; 3);(0; 2;6);(4;2; 6)g solution: denote u = (0;1; 3), v = (0; 2;6), w = (4;2; 6). note that v = 2u and u;w are linearly independent (not parallel to each other), thus the set of all linear combination of u;v;w is two dimensional, i.e. a plane. (b) f(2;1;0);(1;1;1);(4;3;2)g solution: denote u = (2;1;0), v = (1;1;1), w = (4;3;2). Our expert help has broken down your problem into an easy to learn solution you can count on. question: (4) (3 marks) let u = [3, 2, 1] and v= [1, 3, 2] be two vectors in z. find all scalars b in z5 such that (u bv) • (bu v) = 1. (5) (3 marks) let v = [2,0,−1] and w = [0, 2,3].
