
Solved Let U 5 4 And V 1 2 Find 2u 3v U Chegg Express u v in the form a,b . u v= (simplify your answers.) your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. The dot product of u → and v →, denoted u → ⋅ v →, is u → ⋅ v → = u 1 v 1 u 2 v 2 u 3 v 3. note how this product of vectors returns a scalar , not another vector. we practice evaluating a dot product in the following example, then we will discuss why this product is useful.
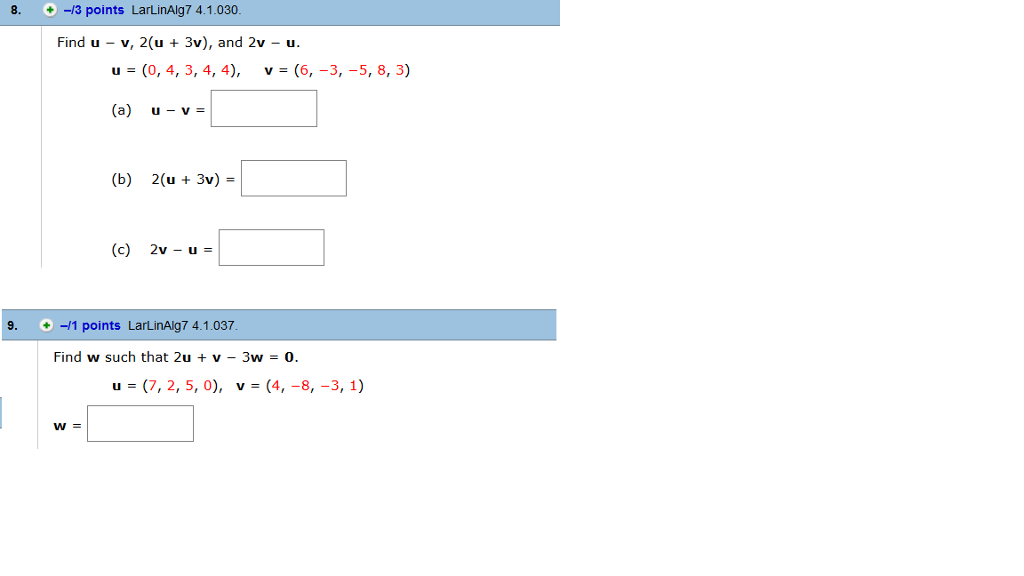
Solved Find U V 2 U 3v And 2v U U 0 4 3 4 Chegg There are 2 steps to solve this one. 13.1.24 let u = (3, 4) and v= ( 3, 5). express u v in the form (a,b). u y= (simplify your answers.) let u = (9,10) and v= (3,9). express 6u 7v in the form (a,b). 6u 7v= {id) (simplify your answers.) let u = (7, 4), v= ( 6,5), and w= (0, 2). Let v be the set of all ordered pairs of real numbers, and consider the following addition and scalar multiplication operations on u = (u1, u2) and v = (v1, v2): compute u v and ku for u = (−1, 2), v = (3, 4) and k = 3. explain in words why v is closed under addition and scalar multiplication. Let u = (3, 2) and v = ( 3, 4) express u v in the form (a, b) u v = (simplify your answers) your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Let u = (5, 3, 21), v = (2, 4, 4), and w = (5, 2, 5). a vector with integer components perpendicular to u and w is: step by step solved, expert educator: let u = (5, 2) and v = ( 4, 10).
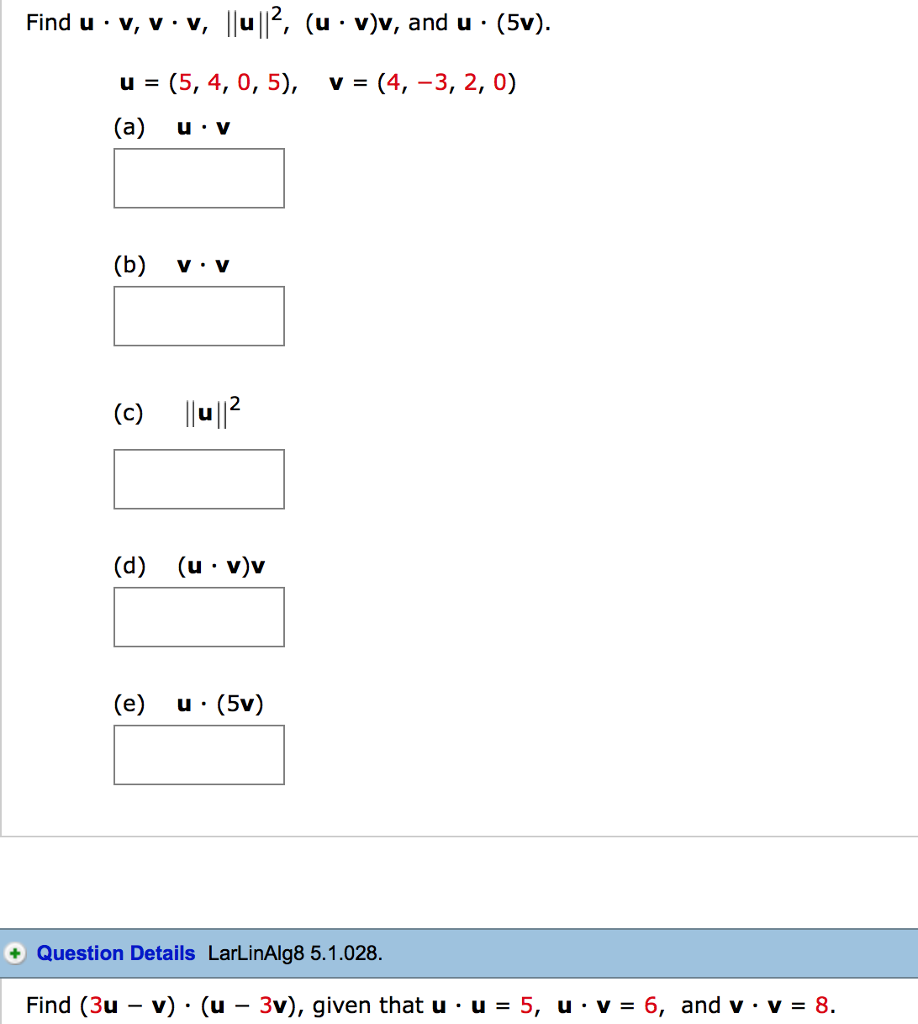
Solved Find U V V V U 2 U V V And U 5v U 5 4 Chegg Let u = (3, 2) and v = ( 3, 4) express u v in the form (a, b) u v = (simplify your answers) your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Let u = (5, 3, 21), v = (2, 4, 4), and w = (5, 2, 5). a vector with integer components perpendicular to u and w is: step by step solved, expert educator: let u = (5, 2) and v = ( 4, 10). Find the vector x that satisfies 3 u − v x =4 x w. there are 2 steps to solve this one. given three vectors u ― = 5, 4 , v ― = 1, − 4 , w ― = 3, 5 . (1 point) let t (5,4), u = 〈1, 4), and w (3,5). find the vector z that satisfies in this case, z = not the question you’re looking for? post any question and get expert help quickly. Let c1, c2 and c3 be positive real numbers and let u = (u1, u2, u3) and v = (v1, v2, v3). show that < u, v >= c1u1v1 c2u2v2 c3u3v3 is an inner product in r3. we need to check the 4 properties. < u, v >=< v, u > this is clear since it is true for multiplication. To check that u v = v u (axiom 3) for w because this holds for all vectors in v and consequently holds for all vectors in w. likewise, axioms 4, 7, 8, 9 and 10 are inherited by w from v. thus to show that w is a subspace of a vector space v (and hence that w is a vector space), only axioms 1, 2, 5 and 6 need to be verified. the. Using this knowledge, we can calculate 3u 5v based on the following. 3u 5v = 3*< 5, 3> 5*< 6, 1> = <15, 9> < 30, 5> = < 15, 4> your answer is correct! when we have vectors that are given in the format of a = 5i 7j, we can rewrite these as a = <5, 7>. using this fact, we can rewrite a and b as the following: a = <5, 7> b = < 4, 3>.

Solved Exercise 7let U 2432435 V 2461735 W 2405235 Chegg Find the vector x that satisfies 3 u − v x =4 x w. there are 2 steps to solve this one. given three vectors u ― = 5, 4 , v ― = 1, − 4 , w ― = 3, 5 . (1 point) let t (5,4), u = 〈1, 4), and w (3,5). find the vector z that satisfies in this case, z = not the question you’re looking for? post any question and get expert help quickly. Let c1, c2 and c3 be positive real numbers and let u = (u1, u2, u3) and v = (v1, v2, v3). show that < u, v >= c1u1v1 c2u2v2 c3u3v3 is an inner product in r3. we need to check the 4 properties. < u, v >=< v, u > this is clear since it is true for multiplication. To check that u v = v u (axiom 3) for w because this holds for all vectors in v and consequently holds for all vectors in w. likewise, axioms 4, 7, 8, 9 and 10 are inherited by w from v. thus to show that w is a subspace of a vector space v (and hence that w is a vector space), only axioms 1, 2, 5 and 6 need to be verified. the. Using this knowledge, we can calculate 3u 5v based on the following. 3u 5v = 3*< 5, 3> 5*< 6, 1> = <15, 9> < 30, 5> = < 15, 4> your answer is correct! when we have vectors that are given in the format of a = 5i 7j, we can rewrite these as a = <5, 7>. using this fact, we can rewrite a and b as the following: a = <5, 7> b = < 4, 3>.
