Solved Let U A B C D E F G M C E G N B Chegg
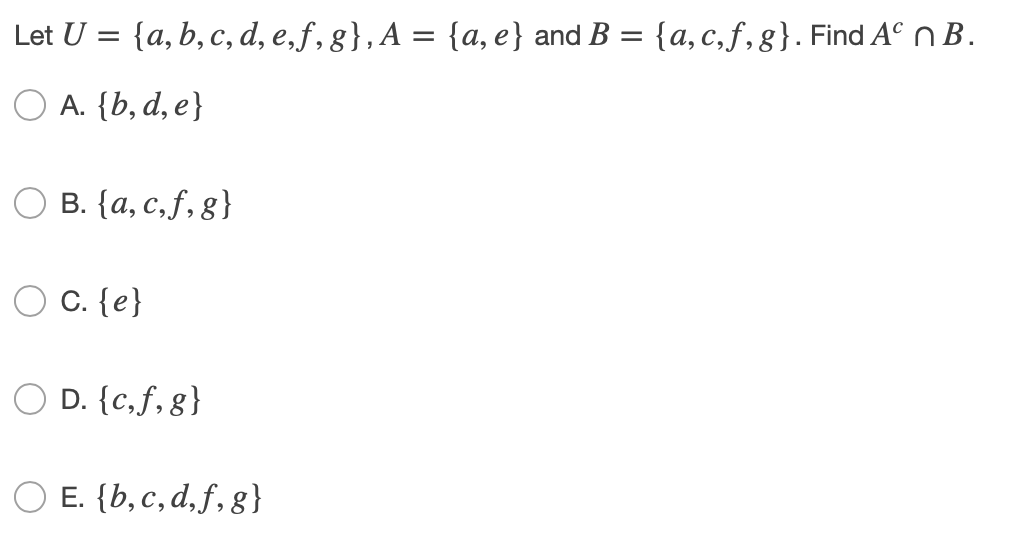
Solved Let U A B C D E F G A A E And B Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. there are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Buc is the union of the two sets b and c. the union contains all the elements that belong to b or c (or both). so in this case, it would be (a,g,i,j,k,e,h) a b is a modification of a set by removing the elements of b from the set a. so a b= {b,c,d,e,f) while (a b) c= {b,c,d,f} still looking for help? get the right answer, fast.

Solved Let U A B C D E F G H I J K A A Chegg Ai explanations are generated using openai technology. ai generated content may present inaccurate or offensive content that does not represent symbolab's view. learning math takes practice, lots of practice. just like running, it takes practice and dedication. if you want. Determine which of the following sets equals (m ∪ n)’. you can put this solution on your website! s = {a, b, c, d, m}. find l’∪ s’. n = {5, 6, 9}. Step by step video, text & image solution for let a= {a,b,c,d,e,f}, b= {c,d,e,g} and c = {b,c,f,g} be subsets of the set u= {a,b,c,d,e,f,g,h}. To find the set a∪(b∩c), we'll first need to determine the intersection of sets b and c, and then take the union of that result with set a. set intersection means we find the elements that are in both sets.

Question Chegg Step by step video, text & image solution for let a= {a,b,c,d,e,f}, b= {c,d,e,g} and c = {b,c,f,g} be subsets of the set u= {a,b,c,d,e,f,g,h}. To find the set a∪(b∩c), we'll first need to determine the intersection of sets b and c, and then take the union of that result with set a. set intersection means we find the elements that are in both sets. There are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. Find step by step statistics solutions and your answer to the following textbook question: let u= {a, b, c, d, e, f, g}, a= {a, b, f, g}, b= {c, d, e}, c= {a, g}, and d= {a, b, c, d, e, f}. To verify the equation (a∩b)′ =(a′∪b′), we will follow a step by step approach. given the universal set u = {a,b,c,d,e,f,g}, and the subsets a= {a,b,d,e} and b = {b,e,g}. common elements in a and b are b and e. therefore, a∩b= {b,e}. u −(a∩b)= u −{b,e}= {a,c,d,f,g}. thus, (a∩b)′ = {a,c,d,f,g}. u −a= u −{a,b,d,e} = {c,f,g}. The final result of the expression (a′ ∪c) ∪(a ∩b) is the universal set u = {a,b,c,d,e,f,g,h,i,j,k}. this is obtained by first calculating the complement of a, the intersection of a and b, and then the union of these results with set c. ultimately, it combines all unique elements from these sets.
Comments are closed.