
Solved Let U1 U2 And V1 V2 Be Ordered Bases For R2 Chegg Let u1=⎣⎡−61−6261⎦⎤ and u2=⎣⎡−305302−301⎦⎤. note that {u1,u2} is an orthonormal set. find a third vector u3 that "extends" {u1,u2} to a full orthonormal basis for r3. that is, construct a vector u3 such that {u1,u2,u3} is an orthonormal basis for r3. your solution’s ready to go!. We can choose any two of the three coordinates to find our desired contradiction. let us, for instance, take the first and second coordinates: „2 3i”= 12 5i and „5 4i”= 7 22i: so, from the first coordinates, we get 13 = „„2 3i”„2 3i”” = „ „2 3i””„2 3i” = „12 5i”„2 3i” = 39 26i.
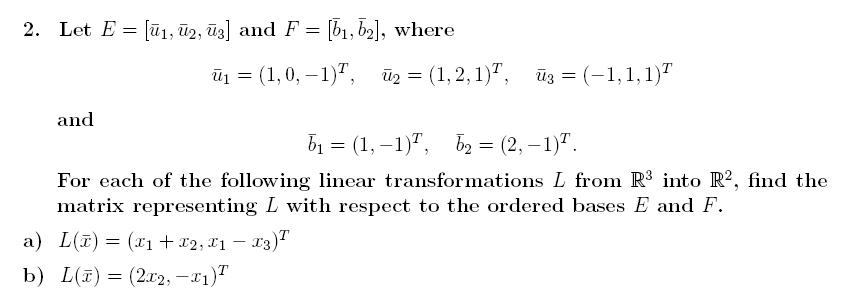
Solved Let E U1 U2 U3 And F B1 B2 Where U1 Chegg Free math problem solver answers your algebra homework questions with step by step explanations. Let v1 = (4,6,7)t, v2 = (0,1,1)t, and v3 = (0,1,2)t. let u1, u2, and u3 be the vectors given in exercise 5. find the transition matrix from v1, v2, v3 to u1, u2, u3. 2. if x = 2v1 3v2 v3,. 1. we know that u1 and u2 are orthogonal, which means their dot product is zero. step 2 8 2. we also know that u3 is not in the subspace w spanned by u1 and u2, which means u3 is not a linear combination of u1 and u2. step 3 8 3. therefore, u3 must have a component that is orthogonal to both u1 and u2. step 4 8 4. Stack exchange network. stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers visit stack exchange.

рџ џрџџ Noches De Milagros Con El Pastor Mariano Riscajche рџ рџ Youtube 1. we know that u1 and u2 are orthogonal, which means their dot product is zero. step 2 8 2. we also know that u3 is not in the subspace w spanned by u1 and u2, which means u3 is not a linear combination of u1 and u2. step 3 8 3. therefore, u3 must have a component that is orthogonal to both u1 and u2. step 4 8 4. Stack exchange network. stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers visit stack exchange. Let u1=⎣⎡−61−6261⎦⎤ and u2=⎣⎡−305302−301⎦⎤. note that {u1,u2} is an orthonormal set. find a third vector u3 that "extends" {u1,u2} to a full orthonormal basis for r3. that is, construct a vector u3 such that {u1,u2,u3} is an orthonormal basis for r3. your solution’s ready to go!. To construct a nonzero vector v in r^3 that is orthogonal to u1 and u2, we can use the fact that u4 is not in the subspace w spanned by u1 and u2. given: u1 = [1, 2, 1] u2 = [2, 1, 2] u4 = [1, 1, 3] step 1: find a vector w that is orthogonal to both u1 and u2 since u4 is not in the subspace spanned by u1 and u2, we can use u4 as a candidate. Let u1 and u2 be independent random variables. suppose that u1 is x2 with v1 degrees of freedom while u = u1 u2 is chi square with v degrees of freedom, where v > v1. then prove that u2 is. Algorithm 17.8 (gram schmidt). let v 1;v 2;:::;v n be independent vectors in a real inner product space v. (1) let 1 k nbe the largest index such that v 1;v 2;:::;v k are orthonormal. (2) if k= mthen stop. (3) otherwise let u k 1 = v k 1 r 1v 1 r 2v 2 r mv m; where r i = hv k 1;v ii. replace v k 1 by u k 1 ku k 1k; and return to (1). in.

Https Yandex Ru Video Touch Preview Filmid 3526456850113939854 Url Let u1=⎣⎡−61−6261⎦⎤ and u2=⎣⎡−305302−301⎦⎤. note that {u1,u2} is an orthonormal set. find a third vector u3 that "extends" {u1,u2} to a full orthonormal basis for r3. that is, construct a vector u3 such that {u1,u2,u3} is an orthonormal basis for r3. your solution’s ready to go!. To construct a nonzero vector v in r^3 that is orthogonal to u1 and u2, we can use the fact that u4 is not in the subspace w spanned by u1 and u2. given: u1 = [1, 2, 1] u2 = [2, 1, 2] u4 = [1, 1, 3] step 1: find a vector w that is orthogonal to both u1 and u2 since u4 is not in the subspace spanned by u1 and u2, we can use u4 as a candidate. Let u1 and u2 be independent random variables. suppose that u1 is x2 with v1 degrees of freedom while u = u1 u2 is chi square with v degrees of freedom, where v > v1. then prove that u2 is. Algorithm 17.8 (gram schmidt). let v 1;v 2;:::;v n be independent vectors in a real inner product space v. (1) let 1 k nbe the largest index such that v 1;v 2;:::;v k are orthonormal. (2) if k= mthen stop. (3) otherwise let u k 1 = v k 1 r 1v 1 r 2v 2 r mv m; where r i = hv k 1;v ii. replace v k 1 by u k 1 ku k 1k; and return to (1). in.
проектная документация неадресная система пожарной сигнализации для Let u1 and u2 be independent random variables. suppose that u1 is x2 with v1 degrees of freedom while u = u1 u2 is chi square with v degrees of freedom, where v > v1. then prove that u2 is. Algorithm 17.8 (gram schmidt). let v 1;v 2;:::;v n be independent vectors in a real inner product space v. (1) let 1 k nbe the largest index such that v 1;v 2;:::;v k are orthonormal. (2) if k= mthen stop. (3) otherwise let u k 1 = v k 1 r 1v 1 r 2v 2 r mv m; where r i = hv k 1;v ii. replace v k 1 by u k 1 ku k 1k; and return to (1). in.

Secret Key Systems Block Encoding Ppt Download
