Solved Let V Be A Vector Space And Let T V V Be A Linear Chegg

Solved Let V Be A Vector Space U U E V And Let T1 V V Chegg Let v,w, and z be vector spaces, and let t:v→w and u:w→z be linear. (a) prove that if ut is one to one, then t is one to one. must u also be one to one? (b) prove that if ut is onto, then u is onto. must t also be onto? (c) prove that if u and t are. your solution’s ready to go!. You've shown that $t$ is identity when restricted to the subspace $f (t)$, which is quite distinct from being the identity map on $v$. think about the intersection $f (t) \cap n (t)$, and what this means geometrically.
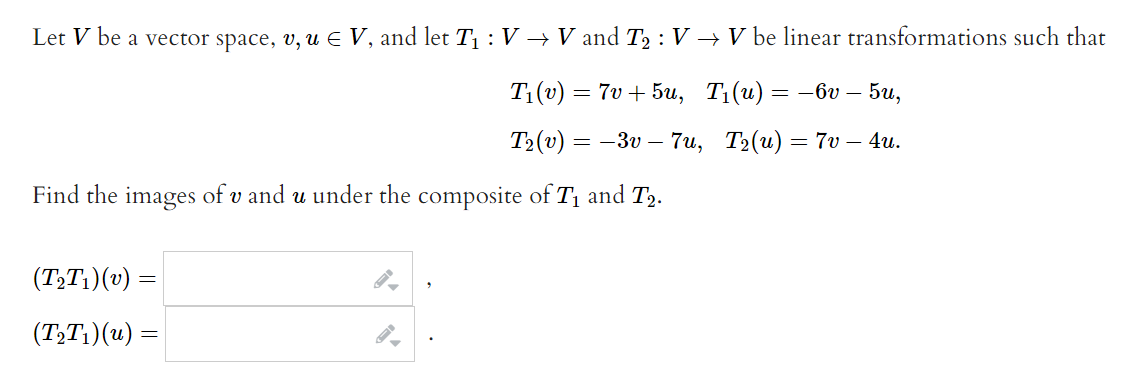
Solved Let V Be A Vector Space V Uв V And Let T1 Vв V And Chegg (5.3) v1 v2 () v1 v2 2 s is an equivalence relation and that the set of equivalence classes, denoted usually v=s; is a vector space in a natural way. problem 5.4. in case you do not know it, go through the basic theory of nite dimensional vector spaces. 6.2 let v and w be vector spaces over f, and suppose that t 2 l(v, w) is injective. given a linearly independent list (v1, , vn) of vectors in v , prove that the list (t(v1), , t(vn)) is linearly independent in w. Prove the infinite dimensional version of the extension theorem: if x is a linearly independent subset of a vector space v, then there exists a basis of v which contains x. Let v be a vector space, and let t: v → v be linear. a subspace w of v is said to be t invariant if t (x) ∈ w for every x ∈ w, i.e., t (w) ⊆ w. (a) prove that the subspaces {0}, v, r (t), and n (t) are all t invariant.
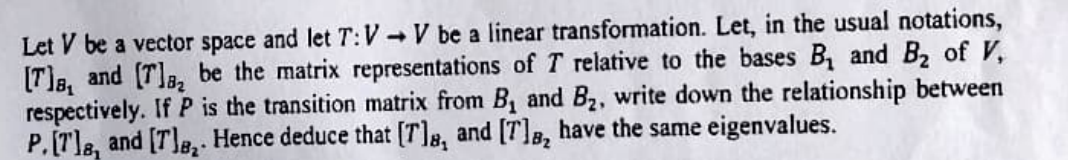
Solved Let V ï Be A Vector Space And Let T Vâ V ï Be A Linear Chegg Prove the infinite dimensional version of the extension theorem: if x is a linearly independent subset of a vector space v, then there exists a basis of v which contains x. Let v be a vector space, and let t: v → v be linear. a subspace w of v is said to be t invariant if t (x) ∈ w for every x ∈ w, i.e., t (w) ⊆ w. (a) prove that the subspaces {0}, v, r (t), and n (t) are all t invariant. To prove that the range space r (t) of a linear transformation t: v → w is a subspace of w, we need to show that it satisfies the three conditions of a subspace: closure under addition, closure under scalar multiplication, and contains the zero vector. let's consider two vectors u and v in r (t). A vector space \ (v\) is a set of vectors with two operations defined, addition and scalar multiplication, which satisfy the axioms of addition and scalar multiplication. Question: let v be a vector space, and t:v→v a linear transformation such that t (2v1 3v2)=−5v1 4v2 and t (3v1 5v2)=−2v1−3v2. then t (v1)=v1 v2. t (v2)=v1 v2 t (−4v1 2v2)=v1 v2. note: you can earn partial credit on this probiem. In our exercise, we consider a vector space denoted by v with a basis of three vectors: {v 1, v 2, v 3}. this setup is crucial for demonstrating properties like linear independence and span, which are essential for understanding other mathematical concepts.

Solved 9 Let V Be A Vector Space With Dimension N Let T V Chegg To prove that the range space r (t) of a linear transformation t: v → w is a subspace of w, we need to show that it satisfies the three conditions of a subspace: closure under addition, closure under scalar multiplication, and contains the zero vector. let's consider two vectors u and v in r (t). A vector space \ (v\) is a set of vectors with two operations defined, addition and scalar multiplication, which satisfy the axioms of addition and scalar multiplication. Question: let v be a vector space, and t:v→v a linear transformation such that t (2v1 3v2)=−5v1 4v2 and t (3v1 5v2)=−2v1−3v2. then t (v1)=v1 v2. t (v2)=v1 v2 t (−4v1 2v2)=v1 v2. note: you can earn partial credit on this probiem. In our exercise, we consider a vector space denoted by v with a basis of three vectors: {v 1, v 2, v 3}. this setup is crucial for demonstrating properties like linear independence and span, which are essential for understanding other mathematical concepts.
Comments are closed.