Solved 2 Let The Universal Set Be Z The Set Of All Integers Chegg Here’s the best way to solve it. let z be the set of all integers and c* be the set of all nonzero complex numbers z = (z, ) together with integer addition is a group, and c* = (c*, 🙂 together with the complex number multiplication is a group. = = let g = {exi|0 sk < 14}. Answer step by step video & image solution for let z be the set of all integers and z 0 be the set of all non zero integers.
Solved 2 Let Z Be The Set Of Integers And Define The Chegg Step 1 4first, let's recall the definition of a partition of a set. a partition of a set s is a collection of non empty, pairwise disjoint subsets of s whose union is equal to s. Find step by step discrete math solutions and your answer to the following textbook question: let $\mathbf {z}$ denote the set of integers, let $\mathbf {z}^ {*}$ denote the set of nonzero integers, and let $\mathbf {q}$ be the set of all rational numbers. Prove that $\equiv$ is an equivalence relation on $z$ and exhibit all the different equivalence sets. well i know there should be $5$ equivalence sets. also, to prove that $a\equiv b$, i have to us. Let z denote the set of integers, let z* denote the set of nonzero integers, and let q be the set of all rational numbers. define a function g : z x z" q by g (a, b) = a b. explain why g is not one to one. be specific. o there are decimals such as 1.425 e q but that do not have an (a, b) e z x z* such that g (a, b) = 1.425.
Solved Suppose Z Denotes The Set Of All Integers Z Chegg Prove that $\equiv$ is an equivalence relation on $z$ and exhibit all the different equivalence sets. well i know there should be $5$ equivalence sets. also, to prove that $a\equiv b$, i have to us. Let z denote the set of integers, let z* denote the set of nonzero integers, and let q be the set of all rational numbers. define a function g : z x z" q by g (a, b) = a b. explain why g is not one to one. be specific. o there are decimals such as 1.425 e q but that do not have an (a, b) e z x z* such that g (a, b) = 1.425. Let a relation r on z × z 0 be defined as (a, b) r (c, d) ⇔ ad = bc for all (a, b), (c, d) ∈ z × z 0, prove that r is an equivalence relation on z × z 0. Step by step video, text & image solution for let z be the set of all integers, then , the operation * on z defined by a*b=a b ab is by maths experts to help you in doubts & scoring excellent marks in class 12 exams. Q7. for n ∈ n let sn = {z ∈ c; |z 3 2i| = n 4} and tn = {z ∈ c : |z 2 3i| = 1 n} then the number of elements in the set {n ∈ n : sn ∩ tn = ϕ} is q8. let α and β be the sum and the product of all the non zero solutions of the equation (z̅)2 |z| = 0, z ∈ c. then 4 (α2 β2) is equal to: q9. Let `zz` be the set of all integers,
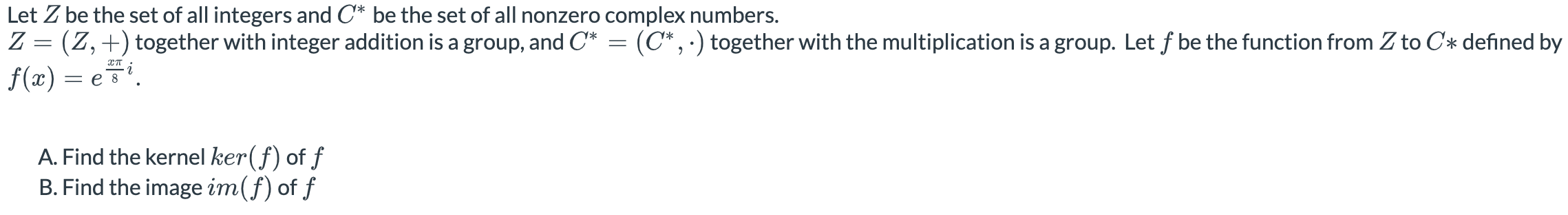
Solved Let Z Be The Set Of All Integers And Cв Be The Set Of Chegg Let a relation r on z × z 0 be defined as (a, b) r (c, d) ⇔ ad = bc for all (a, b), (c, d) ∈ z × z 0, prove that r is an equivalence relation on z × z 0. Step by step video, text & image solution for let z be the set of all integers, then , the operation * on z defined by a*b=a b ab is by maths experts to help you in doubts & scoring excellent marks in class 12 exams. Q7. for n ∈ n let sn = {z ∈ c; |z 3 2i| = n 4} and tn = {z ∈ c : |z 2 3i| = 1 n} then the number of elements in the set {n ∈ n : sn ∩ tn = ϕ} is q8. let α and β be the sum and the product of all the non zero solutions of the equation (z̅)2 |z| = 0, z ∈ c. then 4 (α2 β2) is equal to: q9. Let `zz` be the set of all integers,
Comments are closed.