Solved N Th Term Of An Ap Is Given By An Expression 7n 2 Find The This calculator can be used to determine the expression for the nth term in a given sequence. additionally, it will tell you whether the sequence is arithmetic, geometric, quadratic or neither of these. N^(th) term of an ap is given by an expression 7n 2 , find the common difference of this sequence if first term of sequence is 1? a. 2 b. 2 c. 7 d. 7.
Solved N Th Term Of An Ap Is Given By An Expression 7n 2 Find The A n = n th term that has to be found; a 1 = 1 st term in the sequence; n = number of terms; d = common difference; s n = sum of n terms; a few solved problems on the arithmetic sequence are given below. solved examples using arithmetic sequence formula. question 1: find the 16 th term in arithmetic sequence 0, 2, 4, 6, 8, 10, 12, 14… solution:. This online tool can help you find n th term and the sum of the first n terms of an arithmetic progression. also, this calculator can be used to solve much more complicated problems. for example, the calculator can find the common difference (d) if a 5 = 19 and s 7 = 105. The formula for finding the n th term of an ap is: where. a = first term. d = common difference. n = number of terms. a n = nth term. example: find the nth term of ap: 1, 2, 3, 4, 5…., an, if the number of terms are 15. solution: given, ap: 1, 2, 3, 4, 5…., an. n=15. To find the nth term from the end of the a.p., consider an a.p. where: the a.p. has m terms. the n th term from the end is equivalent to the (m − n 1)th term from the beginning. using the formula for the k th term of an a.p. (ak = a (k − 1)d, the n th term from the end can be written as: am n 1 = a (m – n)d.
Solved Q7 An Expression For The Th Term Of A Sequence Is 7n 3 Find A The formula for finding the n th term of an ap is: where. a = first term. d = common difference. n = number of terms. a n = nth term. example: find the nth term of ap: 1, 2, 3, 4, 5…., an, if the number of terms are 15. solution: given, ap: 1, 2, 3, 4, 5…., an. n=15. To find the nth term from the end of the a.p., consider an a.p. where: the a.p. has m terms. the n th term from the end is equivalent to the (m − n 1)th term from the beginning. using the formula for the k th term of an a.p. (ak = a (k − 1)d, the n th term from the end can be written as: am n 1 = a (m – n)d. For a given arithmetic sequence, the n th term of ap is calculated using the following expression: a n = a (n 1) d. where, let's take an example to understand this. example: find the 25 th term of the given arithmetic sequence 3, 9, 15, 21, 27, … solution: a = 3, d = 6, n = 25. thus, substituting these values in the formula. a n = a (n 1) d. Understand the arithmetic sequence formula & identify known values to correctly calculate the nth term in the sequence. The possible interpretations of the expression could be. 7n 2. 7(n 2) we know that. a1 = 1. a2 = either. a1 2 = 3. a1 2 = 1. a1 7 = 8. a1 7 = 6. so, we can eliminate both negative answer options, because they would cause only negative sequence elements, but the main expression (neither of the 4 possibilities) does not allow that.
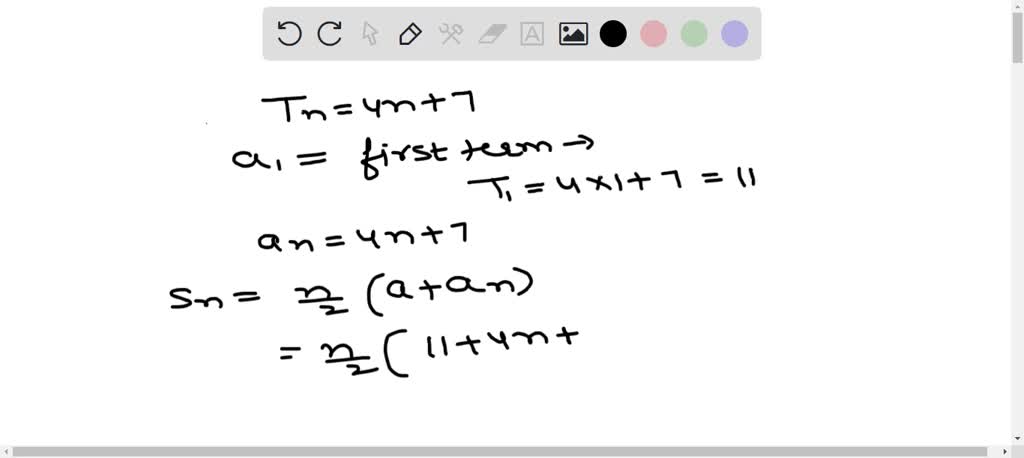
Solved The Nth Term Of An A P Is Given By Tn 4n 7 Find The Sum Of For a given arithmetic sequence, the n th term of ap is calculated using the following expression: a n = a (n 1) d. where, let's take an example to understand this. example: find the 25 th term of the given arithmetic sequence 3, 9, 15, 21, 27, … solution: a = 3, d = 6, n = 25. thus, substituting these values in the formula. a n = a (n 1) d. Understand the arithmetic sequence formula & identify known values to correctly calculate the nth term in the sequence. The possible interpretations of the expression could be. 7n 2. 7(n 2) we know that. a1 = 1. a2 = either. a1 2 = 3. a1 2 = 1. a1 7 = 8. a1 7 = 6. so, we can eliminate both negative answer options, because they would cause only negative sequence elements, but the main expression (neither of the 4 possibilities) does not allow that.

Solved The Nth Term Of An Ap Is Given By An 3 4n The possible interpretations of the expression could be. 7n 2. 7(n 2) we know that. a1 = 1. a2 = either. a1 2 = 3. a1 2 = 1. a1 7 = 8. a1 7 = 6. so, we can eliminate both negative answer options, because they would cause only negative sequence elements, but the main expression (neither of the 4 possibilities) does not allow that.

If The Nth Term Of An Ap Is Given By An 2n 3 Then Common Difference
