Solved A The Number Of Edges In This Graph Is B The Sum Of Chegg Find the number of vertices, the number of edges and the degree of each vertex in the undirected graph. identify all isolated and pendant vertices. find the sum of the degrees of the vertices and verify the handshaking theorem. state explicitly what this is equal to in terms of the edges. Our expert help has broken down your problem into an easy to learn solution you can count on. question: number of edges of the graph vertices of degrees 0,2,2,3, and 9 . how many edges does the graph have? (a) 16 (b) 32 (c) 8 (d) none. there are 2 steps to solve this one. given: the graph having vertices of degrees 0, 2, 2, 3, and 9.
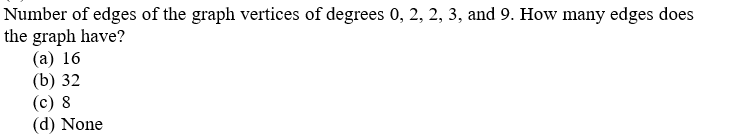
Solved Number Of Edges Of The Graph Vertices Of Degrees Chegg We know that the sum of degree across all nodes is equal to twice the number of edges (handshaking lemma). let there be $n$ vertices in this graph. we have $$ \begin{align} 3 \cdot 4 3 \cdot (n 3) &= 2 \cdot 21 \\ 12 3 \cdot (n 3)&= 42\\ 3 \cdot (n 3)&= 30 \\ (n 3) &= 10\\ n &= 13\\ \end{align} $$. Find the number of vertices, the number of edges, and the degree of each vertex in the given undirected graph. identify all isolated and pendant vertices. find the sum of the degrees of the vertices of the graph. P be the vertices of a graph g, and let d 1,d 2, ,d p be the degrees of the vertices, respectively. let q be the number of edges of g. then d 1 d 2 ··· d p = xp i=1 d i = 2q. note 1.1.a. theorem 1.1.1 is sometimes called “the handshaking lemma” since it implies that in any group of people, an even number of people must have shaken. Let g be an undirected graph. the sum of the degrees of the vertices of g equals twice the number of edges in g. the complete graph on n vertices (denoted kn) is the undirected graph with exactly one edge between every pair of distinct vertices. use the theorem above to derive a formula for the number of edges in kn.

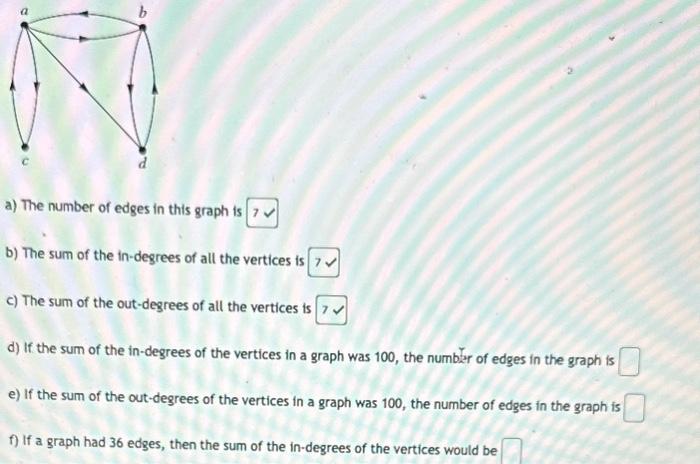
Solved Consider The Following A Give The Number Of Edges Chegg P be the vertices of a graph g, and let d 1,d 2, ,d p be the degrees of the vertices, respectively. let q be the number of edges of g. then d 1 d 2 ··· d p = xp i=1 d i = 2q. note 1.1.a. theorem 1.1.1 is sometimes called “the handshaking lemma” since it implies that in any group of people, an even number of people must have shaken. Let g be an undirected graph. the sum of the degrees of the vertices of g equals twice the number of edges in g. the complete graph on n vertices (denoted kn) is the undirected graph with exactly one edge between every pair of distinct vertices. use the theorem above to derive a formula for the number of edges in kn. In a related theorem, which states that in every graph, the sum of the degrees of all vertices equals twice the number of edges. if there are n vertices vi, v2, so with degrees da, da. du and there are e edges, then 2. In this graph, an even number of vertices (the four vertices numbered 2, 4, 5, and 6) have odd degrees. the sum of degrees of all six vertices is 2 3 2 3 3 1 = 14, twice the number of edges. in graph theory, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number. Determine the sum of the in degrees of the vertices and the sum of the out degrees of the vertices and show that they are both equal to the number of edges in the graph. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. There are 2 steps to solve this one. count the blue lines that connect two black dots, which will represent the number of edges in the graph. an edge of a network is a connection or a link between the vertices of the network. in the figure, th consider the following.

Solved Consider The Following A Give The Number Of Edges Chegg In a related theorem, which states that in every graph, the sum of the degrees of all vertices equals twice the number of edges. if there are n vertices vi, v2, so with degrees da, da. du and there are e edges, then 2. In this graph, an even number of vertices (the four vertices numbered 2, 4, 5, and 6) have odd degrees. the sum of degrees of all six vertices is 2 3 2 3 3 1 = 14, twice the number of edges. in graph theory, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number. Determine the sum of the in degrees of the vertices and the sum of the out degrees of the vertices and show that they are both equal to the number of edges in the graph. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. There are 2 steps to solve this one. count the blue lines that connect two black dots, which will represent the number of edges in the graph. an edge of a network is a connection or a link between the vertices of the network. in the figure, th consider the following.

Solved Consider The Following A Give The Number Of Edges Chegg Determine the sum of the in degrees of the vertices and the sum of the out degrees of the vertices and show that they are both equal to the number of edges in the graph. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. There are 2 steps to solve this one. count the blue lines that connect two black dots, which will represent the number of edges in the graph. an edge of a network is a connection or a link between the vertices of the network. in the figure, th consider the following.

Solved Consider The Following A Give The Number Of Edges Chegg
