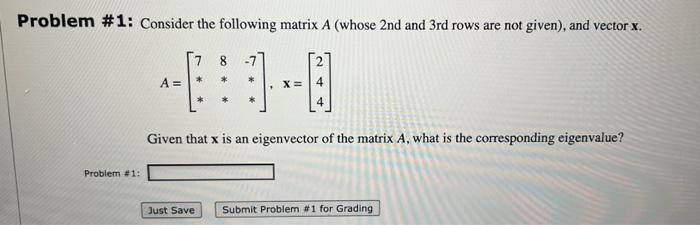
Solved Problem 1 Consider The Following Matrix A Whose Chegg Question: problem \# 1: consider the following matrix a (whose 2 nd and 3rd rows are not given), and vector x. a=⎣⎡7∗∗8∗∗−7∗∗⎦⎤,x=⎣⎡244⎦⎤ given that x is an eigenvector of the matrix a, what is the corresponding eigenvalue?. A from part (a), is the only other matrix whose square is a given by − √ a? why or why not? solution no. we can change some (but not all) of the √ λ i above to − √ λ i, then we will get a new matrix sg √ Λs−1, whose square is a, but it is neither √ a, nor − √ a. so in general there are at least 2n possible matrices whose.

Solved Problem 1 Consider The Following Matrix A Whose Chegg Free math problem solver answers your algebra homework questions with step by step explanations. In this question, we are asked to find the mean return time to state $1$. let $r 1$ be the mean return time to state $1$, i.e., $r 1=e[r|x 0=1]$. then \begin{align*} r 1 &=1 \sum {k} t k p {1k}, \end{align*} where $t k$ is the expected time until the chain hits state $1$ given $x 0=k$. To achieve this, we can use the following row operations: 1. add row 1 to row 2 and replace row 2 with the result. 2. subtract 2 times row 1 to row 3 and replace row 3 with the result. the augmented matrix will now look like: \[ \left(\begin{array}{rrr|r} 1 & 2 & 1 & 1 \\ 0 & 6 & 4 & 3 \\ 0 & 6 & a 2 & 1 \end{array}\right) \]. Our expert help has broken down your problem into an easy to learn solution you can count on. question: problem #7 : consider the following matrix a (whose 2nd and 3rd rows are not given), and vector x. 1 2 10 ホホ given that x is an eigenvector of the matrix a, what is the corresponding eigenvalue?.
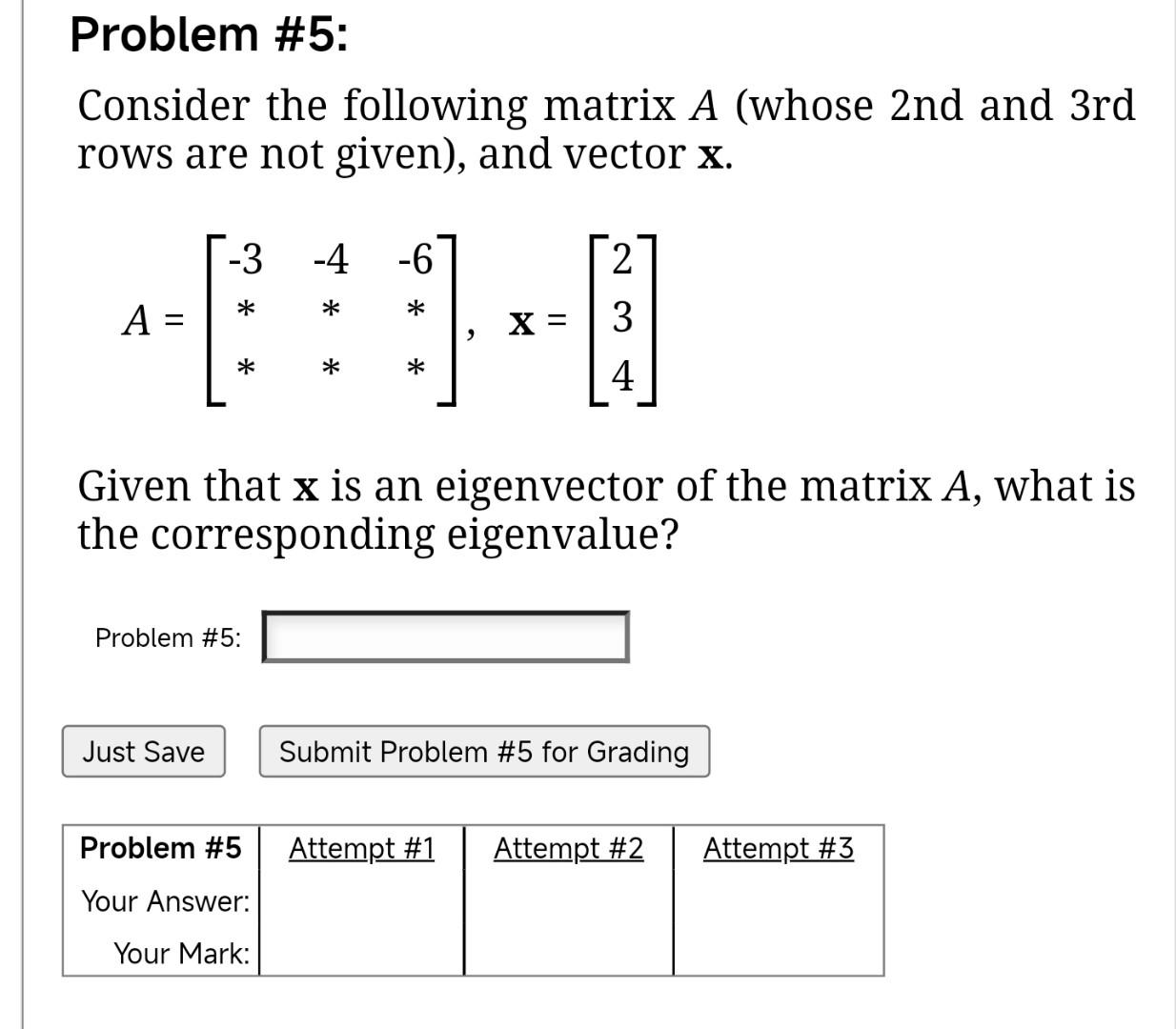
Solved Problem 5 Consider The Following Matrix A Whose Chegg To achieve this, we can use the following row operations: 1. add row 1 to row 2 and replace row 2 with the result. 2. subtract 2 times row 1 to row 3 and replace row 3 with the result. the augmented matrix will now look like: \[ \left(\begin{array}{rrr|r} 1 & 2 & 1 & 1 \\ 0 & 6 & 4 & 3 \\ 0 & 6 & a 2 & 1 \end{array}\right) \]. Our expert help has broken down your problem into an easy to learn solution you can count on. question: problem #7 : consider the following matrix a (whose 2nd and 3rd rows are not given), and vector x. 1 2 10 ホホ given that x is an eigenvector of the matrix a, what is the corresponding eigenvalue?. Matrix problem: function[ok]=first(a,b,x) n = length(a); val = zeros(n,n); flops = 0; for i = 1:n for j = 1:n for k = 1:n val(i,j) = val(i,j) a(i,k)*b(k,i); flops = flops 2; end end end ok = zeros(n,1); for l = 1:n for m = 1:n ok(l)=ok(l) val(l,m)*o. Ans: in each case we seek a = uΣv ∗. the general algorithm is to first find a∗a = (uΣv ∗)∗uΣv ∗ = v Σ∗Σv ∗ = v dv ∗, the spectral decomposition of the hermitian matrix a∗a. then take Σ = √d, noting that Σ may have to be extended to the size of a, i.e. zero rows appended, and solve for u from av = uΣ. Use the geometric interpretation of this transformation as a reflection combined with a scaling to find the eigenvalues of a. b. find two linearly independent eigenvectors for a. Solved problem 3.7. consider a ball in a frictionless cone which is being rotated as shown in figure 2. write down the equations of motion of the ball in the vertical plane.
