Solved Problem 1 Let A1 1 Given An Let An 1 1 Chegg

Solved Problem 1 Let A1 1 Given An Let An 1 1 An 1 2 For Chegg This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. Our expert help has broken down your problem into an easy to learn solution you can count on. question: 1.60. let a= {1, {1}, { {1}}}. determine a×a 1.61. for a= {a,b}, determine a×p (a). 1.62. for a= {∅, {∅}}, determine a×p (a). there are 2 steps to solve this one. 1.60. let a={1,{1},{ {1}}}. determine a×a 1.61.

Solved Problem 1 Given Nв ґ1 And Mв ґ1 Let A1в Rnг N A2в Rmг M Chegg You'll need to complete a few actions and gain 15 reputation points before being able to upvote. upvoting indicates when questions and answers are useful. what's reputation and how do i get it? instead, you can save this post to reference later. Coefficients. the main problem with problem: find a list of n numbers (s1, s2, . . . , sn) that satisfy th. system of linear equa tions (1.1). in other words, if we substitute the list of numbers (s1, s2, . . . , sn) for the unknown variables (x1, x2, . . . , xn) in equation (1.1) then the left hand sid. This can be shown using induction of the form: check for $n=1$ and $n=2$, and then assuming that the statement is true for $n=k$ and $n=k 1$, where $k$ arbitrary, show that it is true for $n=k 2$. Problem 4. let a1 =1 and let an 1 = 31an 1. use induction to show that (an) is monotone and bounded. conclude that (an) is convergent and find the limit. make sure to mention the name of the theorem you are using.

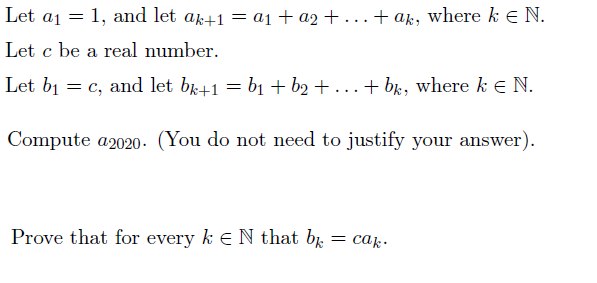
Solved Let A1 1 And Let Ak 1 A1 A2 Ak Where K E Chegg This can be shown using induction of the form: check for $n=1$ and $n=2$, and then assuming that the statement is true for $n=k$ and $n=k 1$, where $k$ arbitrary, show that it is true for $n=k 2$. Problem 4. let a1 =1 and let an 1 = 31an 1. use induction to show that (an) is monotone and bounded. conclude that (an) is convergent and find the limit. make sure to mention the name of the theorem you are using. Let an be given by a0=1,a1=3 and an 1=an 5an−1. prove that an≤3n for all n≥0. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. question: problem 1. let an be given by a0=1,a1=3 and an 1=an 5an−1. prove that an≤3n for all n≥0. there are 4 steps to solve this one. problem 1.