Solved Problem 1 Let X Y E Z Then 4 X Y2 If And Only Chegg

Solved Problem 1 Let X Y E Z Then 4 X Y2 If And Only Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. In order for p to be a generating function of a probability distribution we must have p (1) = 1, i.e. a b c = 1, which will be assumed throughout the problem.

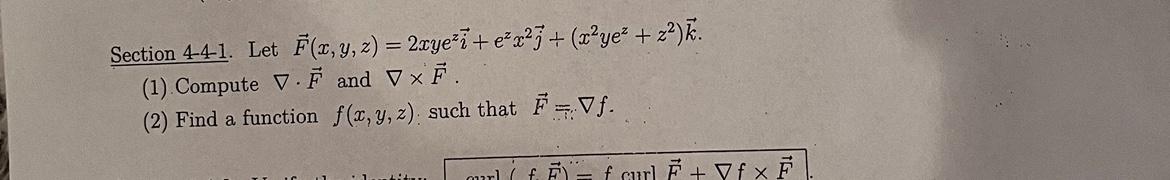
Solved Section 4 4 1 Let F X Y Z 2xyezi Ezx2j X2yez Z2 K Chegg Solution: recall that a function u(x; y) is called harmonic if uxx uyy = 0. so xn yn is harmonic if n(n 1)(xn 2 yn 2) = 0, which means that n = 0, n = 1, or n = 2. Let $x, y$ and $z$ be three independent random variables with $x \sim n (\mu, \sigma^2)$, and $y,z \sim uniform (0,2)$. we also know that \begin {align}%\label {} &e [x^2y xyz]=13, \\ &e [xy^2 zx^2]=14. \end {align} find $\mu$ and $\sigma$. By the associative and identity laws for addition we deduce that (x ( x)) i ( x) x, and hence by the inverses law x. we now use the commutative and identity for addition we see that 0 ( ( x) laws for addition to conclude that ( x) x. Our expert help has broken down your problem into an easy to learn solution you can count on.

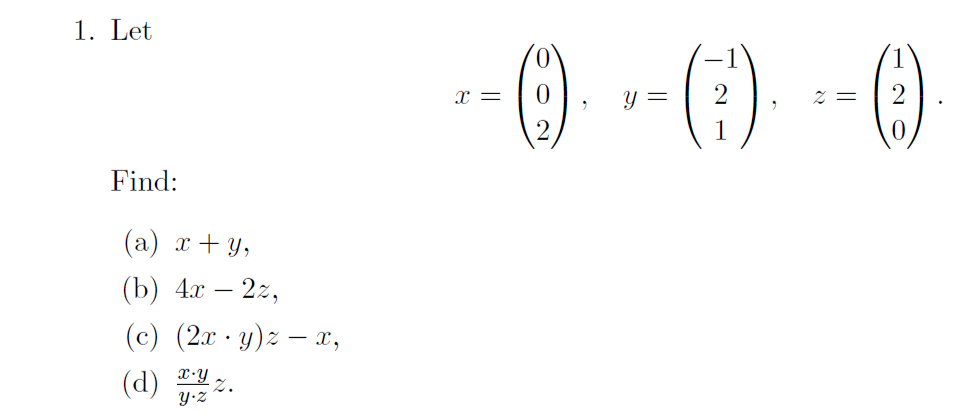
Solved Letx 0 0 2 Y 1 2 1 Z 1 2 0 Chegg By the associative and identity laws for addition we deduce that (x ( x)) i ( x) x, and hence by the inverses law x. we now use the commutative and identity for addition we see that 0 ( ( x) laws for addition to conclude that ( x) x. Our expert help has broken down your problem into an easy to learn solution you can count on. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer. Click on the email ☝️ to watch the video solution. create a free account and get: sign up now!. In this problem, our goal is to find the variance of the hypergeometric distribution. let's remember the random experiment behind the hypergeometric distribution. you have a bag that contains $b$ blue marbles and $r$ red marbles. One approach is to first prove the following “lemma” and then use it to prove the theorem: lemma: let x, y e z. if x² y² is odd, then exactly one of x and y is odd.