Solved Problem 2 17 Determine By Trigonometry The Magnitude And Direction Of The Force P

Chapter 7 Trigonometry And Modelling P2 Pdf Solved problem 2.17 | vector mechanics for engineers statics and dynamics 10th edition beer & johnston: for the stake of prob. 2.5, knowing that the tension in one rope is 120 n,. Knowing that a = 30°, determine by trigonometry (a) the magnitude of the force p so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant. not the question you’re looking for? post any question and get expert help quickly.

Solved Question 3 Determine By Trigonometry The Magnitude Chegg For the hook support of problem 2.1, knowing that the magnitude of p is 75 n, determine (a) the required magnitude of the force q if the resultant r of the two forces applied at a is to be vertical, (b) the corresponding magnitude of r. Knowing that a = 30°, determine by trigonometry (a) the magnitude of the force p so that the resultant force exerted on the stake is vertical, (b) the corresponding magnitude of the resultant. This document contains solutions to 9 problems involving determining the magnitude and direction of the resultant force from two or more applied forces using graphical methods like the parallelogram law and triangle rule, as well as trigonometric methods like the law of sines and cosines. Learn to solve force resultant problems using graphical methods (parallelogram, triangle rule) and trigonometry (law of sines, cosines). ideal for physics and engineering students.

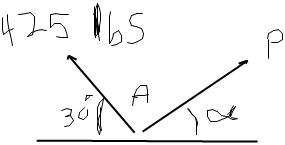
Solved Determine By Trigonometry A The Magnitude And Chegg This document contains solutions to 9 problems involving determining the magnitude and direction of the resultant force from two or more applied forces using graphical methods like the parallelogram law and triangle rule, as well as trigonometric methods like the law of sines and cosines. Learn to solve force resultant problems using graphical methods (parallelogram, triangle rule) and trigonometry (law of sines, cosines). ideal for physics and engineering students. This document contains solutions to 21 problems involving determining the resultant force of two or more applied forces using trigonometry and graphical methods. many of the problems involve forces applied to structural members or supports. Solved problem 2.7 | determine by trigonometry the magnitude and direction of the force p. Using trigonometry, determine (a) the magnitude and direction of the smallest force p for which the resultant r of the two forces applied at a is vertical, (b) the corresponding magnitude of r. solution we observe that force p is minimum when d is 90q, that is, p is horizontal then: (a) p 360 n sin 35q or p and: (b) r 206 n 360 n cos 35q or r. To work with a vector, we need to be able to find its magnitude and its direction. we find its magnitude using the pythagorean theorem or the distance formula, and we find its direction using the inverse tangent function.

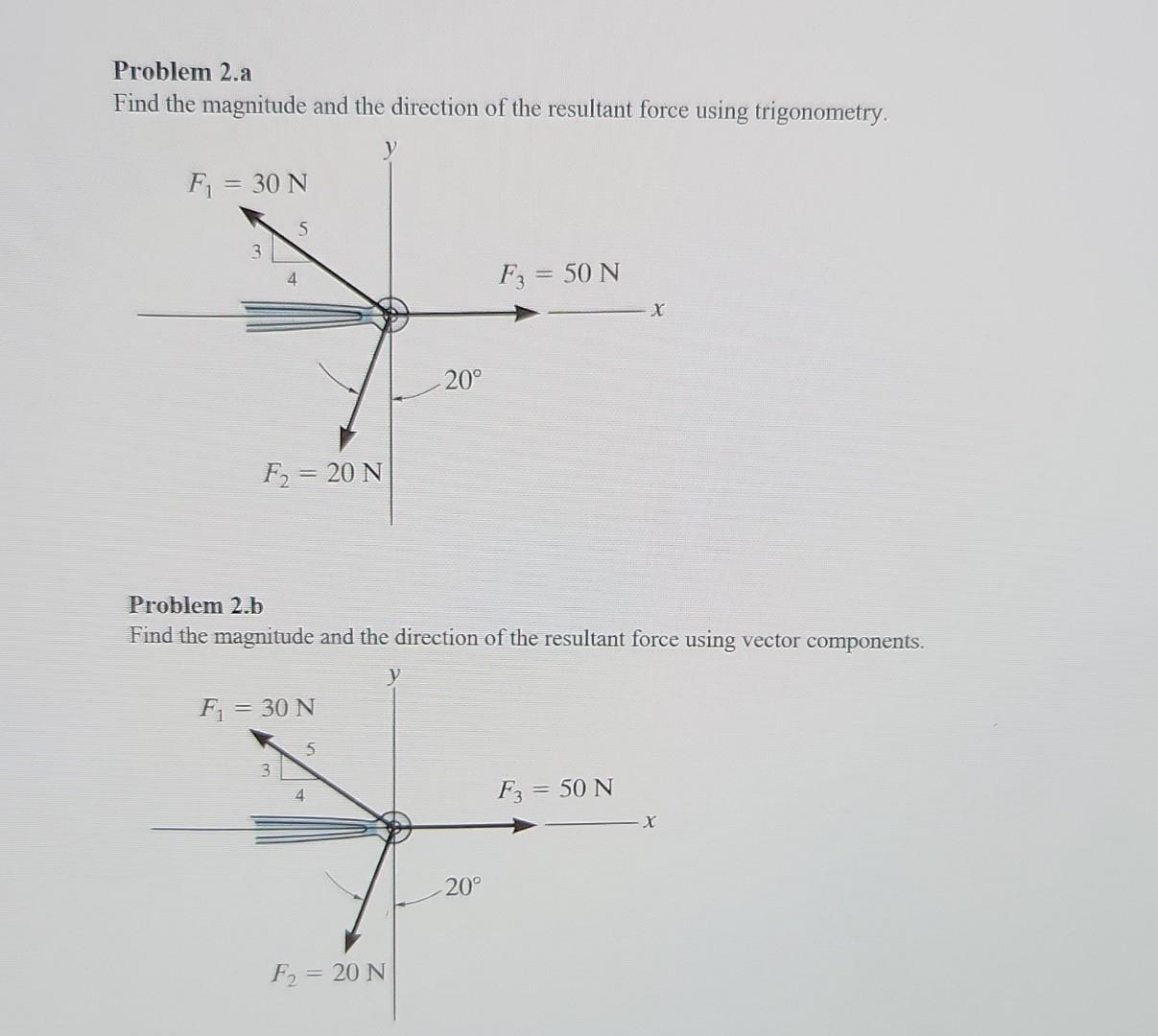
Solved Problem 2 A Find The Magnitude And The Direction Of Chegg This document contains solutions to 21 problems involving determining the resultant force of two or more applied forces using trigonometry and graphical methods. many of the problems involve forces applied to structural members or supports. Solved problem 2.7 | determine by trigonometry the magnitude and direction of the force p. Using trigonometry, determine (a) the magnitude and direction of the smallest force p for which the resultant r of the two forces applied at a is vertical, (b) the corresponding magnitude of r. solution we observe that force p is minimum when d is 90q, that is, p is horizontal then: (a) p 360 n sin 35q or p and: (b) r 206 n 360 n cos 35q or r. To work with a vector, we need to be able to find its magnitude and its direction. we find its magnitude using the pythagorean theorem or the distance formula, and we find its direction using the inverse tangent function.