
Solved Problem Iii 25 Points Apply The Lambert W Function Chegg Answer to solved problem iii (25 points) apply the lambert w function | chegg. Our expert help has broken down your problem into an easy to learn solution you can count on. question: problem 3.5 (lambert w function) consider the function f: rr: 1 h x exp ( ). lim, (i) compute the f'. what are the intervals where f strictly decreases and where strictly increases? does f have minimizers or maximizers?.

Solved Problem 8 6 Lambert W Function Continued Let W Be Chegg A simple equation that turned out to be needing an unfamiliar function to be solved algebraically #algebra | the lambert w function. This problem tests knowledge of advanced algebraic concepts, particularly the application of the lambert w function, which is used to solve equations where the unknown variable appears. Solve the following using lambert's w function: $xe^{2x} = 3$ $x \cdot 3^x = 9$ $x \ln x = \ln 2$ $2^x = 10x$ $x^2 8\ln x = 0$ $x^2 = 2^x$. (ii) consider fl, which is a strictly increasing function. this gives rise to the inverse function w. determine the domain d and the range of w. the function w is also called the lambert w function.

40 Points The Lambert W Function W T Is Defined To Chegg Solve the following using lambert's w function: $xe^{2x} = 3$ $x \cdot 3^x = 9$ $x \ln x = \ln 2$ $2^x = 10x$ $x^2 8\ln x = 0$ $x^2 = 2^x$. (ii) consider fl, which is a strictly increasing function. this gives rise to the inverse function w. determine the domain d and the range of w. the function w is also called the lambert w function. I am looking for a solution to the equation $x\, \exp(poly(x)) = c$ for some polynomial $poly(x)$ in $x$ and a real number $c$. we know that the lambert $w$ function provides an analytical solution to. There are two ways to do this: in some very special cases, one can extract out of w(·) if the dot is one of a few numbers like those we saw above: 0, 1, e, etc, in which case the expression is replaced by a number of some sort. w0(xx 1 ln x) = x ln x . The equation x^x = 25 is a fascinating problem that combines elements of exponential functions, logarithmic manipul. Look at two problems: a) solve =ln( ) b) find the inverse function of ( )= both of these can be solved using the lambert w function. imagine we had some function: ( )= then the lambert w function functions the inverse of this, i.e. if the input is x, then it finds some such that = .
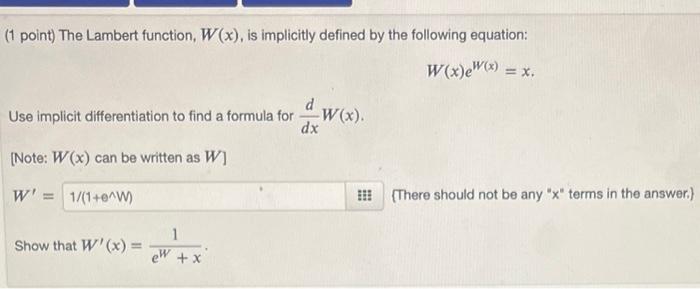
Solved 1 Point The Lambert Function W X Is Implicitly Chegg I am looking for a solution to the equation $x\, \exp(poly(x)) = c$ for some polynomial $poly(x)$ in $x$ and a real number $c$. we know that the lambert $w$ function provides an analytical solution to. There are two ways to do this: in some very special cases, one can extract out of w(·) if the dot is one of a few numbers like those we saw above: 0, 1, e, etc, in which case the expression is replaced by a number of some sort. w0(xx 1 ln x) = x ln x . The equation x^x = 25 is a fascinating problem that combines elements of exponential functions, logarithmic manipul. Look at two problems: a) solve =ln( ) b) find the inverse function of ( )= both of these can be solved using the lambert w function. imagine we had some function: ( )= then the lambert w function functions the inverse of this, i.e. if the input is x, then it finds some such that = .
