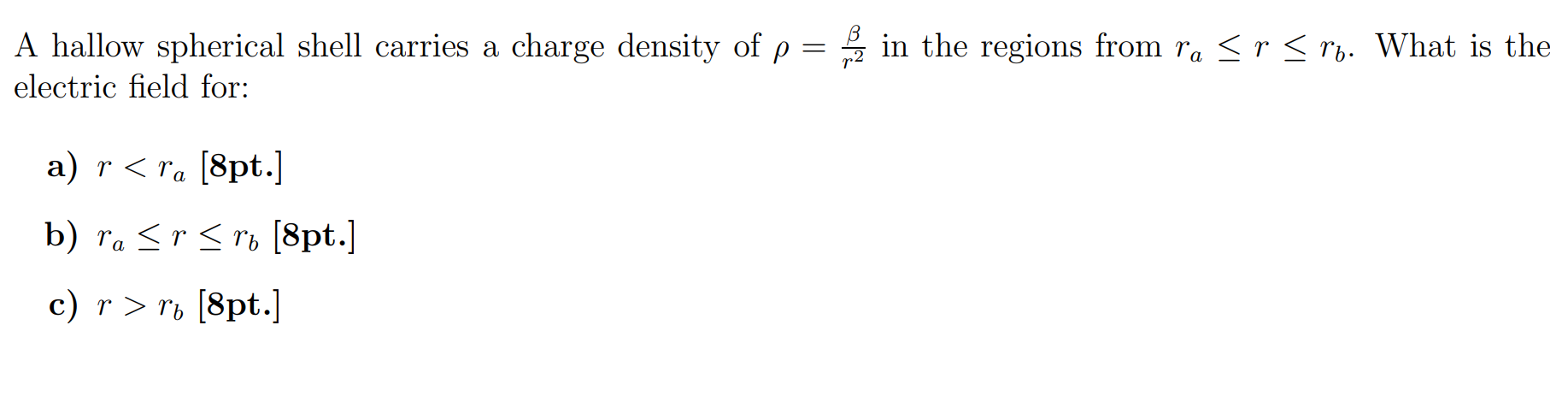
Solved тъ τα Figure 3 Spherical Shell Of Charge A Hallow Chegg Problem4 you have a spherical shell of charge (such as a spherical conductor) with radius r and charge q. suppose the sphere is cut into two hemispheres, so that the two parts are in electric contact by are free to move. the northern hemisphere is lying in the x,y plane and points (domes) towards z. Consider a spherical shell of radius r, carrying a uniform surface charge density σ. the object is spinning at angular velocity ω. a) using an appropriate coordinate system, find the velocity w of a point on the sphere b) show that the vector potential inside and outside the shell is 3r3 c) find the magnetic field inside and outside the shell.

Solved Spherical Shell Charge Consider A Spherical Shell Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly. You have a spherical shell (radius r) which has been covered by some surface charge distribution (o). the potential everywhere is given by outside the shell: voat,0) = (c) coso inside the shell: v.fr.0) (vor r) cose a) given these two formulas, 1 claim the constant "c" in veur) can be immediately deduced. Question: two spherical thin shells of charge both have a center at the origin. shell 2 has radius of r2m and charge density of ρ2=r22cm2 and shell 1 has a radius of r12cm2r1 meters and a charge density of r12cm2.a. meters with each of three faces of the cube being on one of the three planes in the cartesian coordinate. Problem 4.15 a thick spherical shell (inner radius a and outer radius b) is made of dielectric material with a “frozen in” polarization p r k r rÖ. (there is no free charge in the problem.) a. locate all of the bound charge and use gauss’s law to calculate the electric field. the bound volume charge is b p 1 r 2 r 2 p r 1 kr k. on the.

Solved Question Chegg Question: two spherical thin shells of charge both have a center at the origin. shell 2 has radius of r2m and charge density of ρ2=r22cm2 and shell 1 has a radius of r12cm2r1 meters and a charge density of r12cm2.a. meters with each of three faces of the cube being on one of the three planes in the cartesian coordinate. Problem 4.15 a thick spherical shell (inner radius a and outer radius b) is made of dielectric material with a “frozen in” polarization p r k r rÖ. (there is no free charge in the problem.) a. locate all of the bound charge and use gauss’s law to calculate the electric field. the bound volume charge is b p 1 r 2 r 2 p r 1 kr k. on the. A spherical charge cloud (whose center coincides with the origin) with a charge density \rho v = ((1) (r))( c) (m)3 and outer radius r = a is placed in a medium with a dielectric constant of \epsi 1. this structure is surrounded by another perfect dielectric material with \epsi 2 until r = b, where a < b. A spherical shell of radius r has a charge distribution such that the potential at the surface of the sphere is v(r=r, theta) =ksin2 (theta). determine the potential everywhere outside the sphere. your solution’s ready to go!. Problem 4 a thick spherical shell carries a charge density p = k r^2 in the region a leq r leq b. find the electric field in the three regions (i) r < a, (ii) a < r < b, and (iii) r > b. note: the inner and outer regions are vacuum. Here’s the best way to solve it. problem 2 exercises with s functions (i) a charge q is spread uniformly over a spherical shell of radius r. express the charge density using a delta function in spherical coordinates. repeat for a ring of radius r with charge q lying in the xy plane.

Solved Problem4 You Have A Spherical Shell Of Charge Such Chegg A spherical charge cloud (whose center coincides with the origin) with a charge density \rho v = ((1) (r))( c) (m)3 and outer radius r = a is placed in a medium with a dielectric constant of \epsi 1. this structure is surrounded by another perfect dielectric material with \epsi 2 until r = b, where a < b. A spherical shell of radius r has a charge distribution such that the potential at the surface of the sphere is v(r=r, theta) =ksin2 (theta). determine the potential everywhere outside the sphere. your solution’s ready to go!. Problem 4 a thick spherical shell carries a charge density p = k r^2 in the region a leq r leq b. find the electric field in the three regions (i) r < a, (ii) a < r < b, and (iii) r > b. note: the inner and outer regions are vacuum. Here’s the best way to solve it. problem 2 exercises with s functions (i) a charge q is spread uniformly over a spherical shell of radius r. express the charge density using a delta function in spherical coordinates. repeat for a ring of radius r with charge q lying in the xy plane.
