
Solved Prove That 1 X X2 Xn 1 1 Xn 1 X Chegg Assuming that |x| < 1, find the sum of the series 1 x x2 . hint: it is the limit of the finite sum 1 x x2 xn 1 as n rightarrow infinity. find the derivative of exp( x) xk k!. It follows that $$\frac{1 x^{n 1}}{1 x}=1 x x^2 x^3 \cdots x^n$$ as polynomials, because the equality holds for infinitely many values of $x$ (and we are working over $\mathbb z$ ).
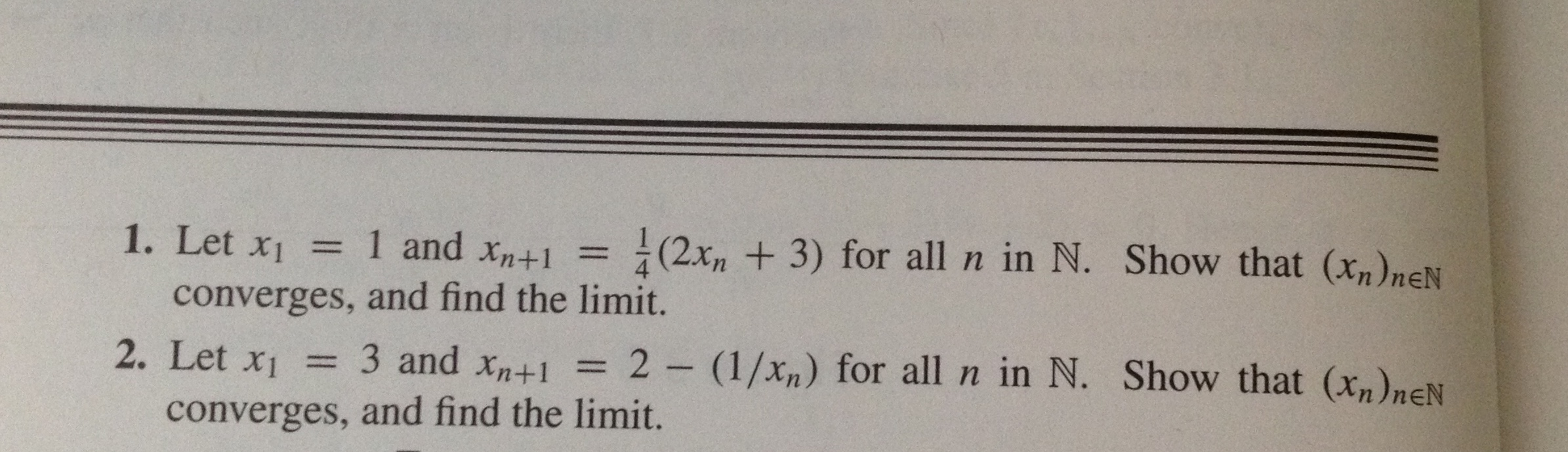
Solved Let X1 1 And Xn 1 1 4 2xn 3 For All N In N Show Chegg Just repeat the proof as in the case n = 2. prove it for n=1; then, assuming that it is true for n=k, try to show that it is true for n=k 1. it is easy indeed. (i do not know the name of this proving method.) to conclude your induction proof, just multiply x both sides : xn − 1 = (x − 1)(xn − 1 xn − 2 x 1) multiply x both sides :. Prove by induction that for each n n 1 x x2 xn 1= (1 xn) (1 x) #1) let x be a real number. suppose that x is not equal to 1. prove by induction that for each n n. there are 3 steps to solve this one. given that x ∈ r such that x ≠ 1. to show by induction that for each n ∈ n, 1 x x 2 … x n − 1 = 1 − x n 1 − x. (a) prove that if x =1, then 1 x x2 ⋯ xn=1−x1−xn 1 (b) use (a) to prove that if ∣x∣<1, then limn→∞(∑j=0nxj)=1−x1. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. There are 2 steps to solve this one. 1 x x2 ⋯ xn = 1−x1−xn 1 if x =1 use this to show that the expansions 1−x1 =1 x x2 x3 ⋯ and 1 x1 =1−x x2−x3 ⋯ are valid for ∣x∣<1. apply the latter to show that log(1 x)=x− 2x2 3x3 − 4x4 ⋯ and tan−1x= x− 3x3 5x5 − 7x7 ⋯ for ∣x∣<1.

Solved Let X1 1 And Xn 1 Xn 2 Xn 0 5 For N 1 Chegg (a) prove that if x =1, then 1 x x2 ⋯ xn=1−x1−xn 1 (b) use (a) to prove that if ∣x∣<1, then limn→∞(∑j=0nxj)=1−x1. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. There are 2 steps to solve this one. 1 x x2 ⋯ xn = 1−x1−xn 1 if x =1 use this to show that the expansions 1−x1 =1 x x2 x3 ⋯ and 1 x1 =1−x x2−x3 ⋯ are valid for ∣x∣<1. apply the latter to show that log(1 x)=x− 2x2 3x3 − 4x4 ⋯ and tan−1x= x− 3x3 5x5 − 7x7 ⋯ for ∣x∣<1. If a 1, a 2, …, a n are sets, prove that a 1 ∪ a 2 ∪ … ∪ a n = a n ∪ a n–1 ∪ … ∪ a 1 where the unions are performed in order from left to right. there are 3 steps to solve this one. To prove the inequality 1 x 1 1 x 2 … 1 x n ≥ n 2 x 1 x 2 … x n, we can use mathematical induction. base case (n = 1): for n = 1, we have 1 x 1 ≥ 1 2 x 1, which is t. Our expert help has broken down your problem into an easy to learn solution you can count on. let x = (xn) be defined by x1= 1 x2 = 2 xn =(xn 2 xn 1) forn>2. there are 2 steps to solve this one. certainly, i can help you with these proofs by mathematical induction. a) proof by induction that 1 < not the question you’re looking for?. Let x1, x2, · · · , xn, · · · be a sequence of integers which is defined as follows: (1) x1 = −1 and x2 = 1, (2) for any n ≥ 3, xn = xn−2 2. find a formula for xn and prove it using mathematical induction.
