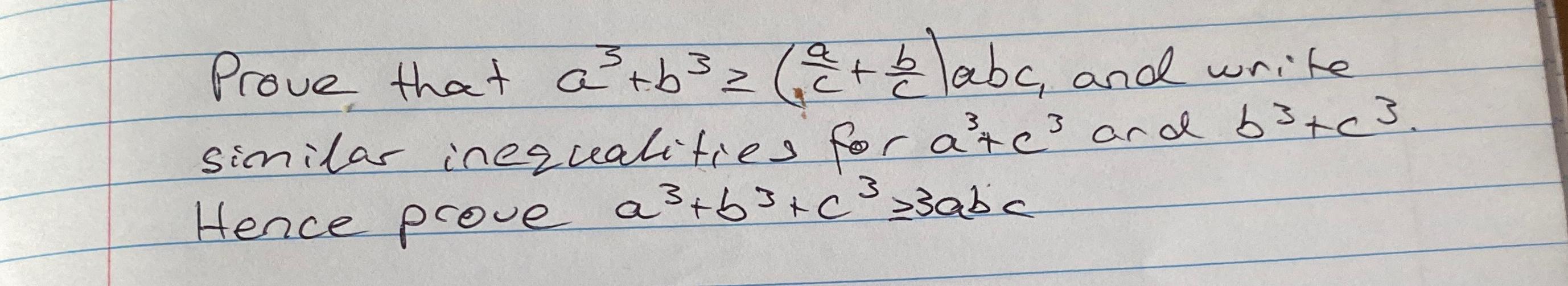
Solved Prove That A3 B3 C3 3abc A B C X Where х Chegg

Solved Prove That A3 B3â Ac Bc Abc ï And Write Similar Chegg Start by expanding the right hand side (rhs) with x = a 2 b 2 c 2 − a b − b c − c a and then distribute the expression (a b c) through it. prove that a3 b3 c3 – 3abc = (a b c) x where Х a 62 62 ab bc c 1 x ( (a b)2 (6–cť (c – a)) x (a bw cw?) (a b2 6w) where w = (2 1 3 ca or or a b с b hint. For complex numbers a a, b b, and c c, a3 b3 c3 = 3abc a b c = 3 a b c if and only if the (possibly degenerate) triangle formed by complex coordinates a a, b b, and c c is an equilateral, or has its centroid at the origin 0 0 (or equivalently, a b c = 0 a b c = 0, a bω cω2 = 0 a b ω c ω = 0, or a bω2 cω = 0 a b ω c.

Solved If A B C 0 ï Prove That A3 B3 C3 3abc Chegg If a b c=0 show that a^3 b^3 c^3=3abc. recognize that $$a b c=0$$a b c = 0, which implies $$a b= c$$a b = −c, $$b c= a$$b c = −a, and $$c a= b$$c a = −b. substitute these into the equation: so, the proof is complete. 😉 want a more accurate answer? get step by step solutions within seconds. Conditions for a = b = c: all values add up to zero: if a b c = 0, then there's a special identity that applies: a³ b³ c³ = 3abc. in this case, if you plug in a = b = c, you'll indeed get a = b = c. special cases with zero and non zero terms: if two variables are zero and the third is non zero, it will automatically satisfy the equation. Prove that \\[{a^3} {b^3} {c^3} 3abc = \\left( {a b c} \\right)\\left( {{a^2} {b^2} {c^2} ab bc ca} \\right)\\] . how can i solve this without expanding everything?. ans: hint: here in this question, we have to prove right hand s. $a^3 b^3 c^3 3abc=(a b c)(a b\omega c\omega^2)(a b\omega^2 c\omega)$, where $\omega$ is the root of $x^2 x 1=0$.

Solved Prove That A3 B3 C3 3abc A B C X Where х Chegg Prove that \\[{a^3} {b^3} {c^3} 3abc = \\left( {a b c} \\right)\\left( {{a^2} {b^2} {c^2} ab bc ca} \\right)\\] . how can i solve this without expanding everything?. ans: hint: here in this question, we have to prove right hand s. $a^3 b^3 c^3 3abc=(a b c)(a b\omega c\omega^2)(a b\omega^2 c\omega)$, where $\omega$ is the root of $x^2 x 1=0$. If a 3 b 3 = c 3 then c 3 a b is rational, while true, makes no sense as a theorem because you only used the fact that they're all integers. and, in the second part, you basically proved if a 3 b 3 = t (a b) 3 then t = 1, which clearly can't be right. Regarding the c 3 = t 3 (a b) 3 argument, you could formulate it as follows. as you say, c 3 = s(a b) for some integer s. then we have that c 3 = t 3 (a b) 3 for t=s (c 2 ). If $a,b,c,d$ are real numbers and $a b c d=0$. prove: $$a^3 b^3 c^3 d^3=3(abc bcd cda dab)$$ using euler's identity: if $x y z=0$ then $x^3 y^3 z^3=3xyz$. in this problem substitute $x=a b,y=c,z= skip to main content. There are 3 steps to solve this one. prove the given inequality (a 3 b 3 ≥ (a c b c) a b c) and then use similar inequalities to derive (a 3 b 3 c 3 ≥ 3 a b c).

Plz Help Prove That A B 3 B C 3 C A 3 3 A B B C If a 3 b 3 = c 3 then c 3 a b is rational, while true, makes no sense as a theorem because you only used the fact that they're all integers. and, in the second part, you basically proved if a 3 b 3 = t (a b) 3 then t = 1, which clearly can't be right. Regarding the c 3 = t 3 (a b) 3 argument, you could formulate it as follows. as you say, c 3 = s(a b) for some integer s. then we have that c 3 = t 3 (a b) 3 for t=s (c 2 ). If $a,b,c,d$ are real numbers and $a b c d=0$. prove: $$a^3 b^3 c^3 d^3=3(abc bcd cda dab)$$ using euler's identity: if $x y z=0$ then $x^3 y^3 z^3=3xyz$. in this problem substitute $x=a b,y=c,z= skip to main content. There are 3 steps to solve this one. prove the given inequality (a 3 b 3 ≥ (a c b c) a b c) and then use similar inequalities to derive (a 3 b 3 c 3 ≥ 3 a b c).

A3 B3 C3 3abc A B C 0 Prove That A B 2 3ab B C 2 3bc C A 2 3ac If $a,b,c,d$ are real numbers and $a b c d=0$. prove: $$a^3 b^3 c^3 d^3=3(abc bcd cda dab)$$ using euler's identity: if $x y z=0$ then $x^3 y^3 z^3=3xyz$. in this problem substitute $x=a b,y=c,z= skip to main content. There are 3 steps to solve this one. prove the given inequality (a 3 b 3 ≥ (a c b c) a b c) and then use similar inequalities to derive (a 3 b 3 c 3 ≥ 3 a b c).

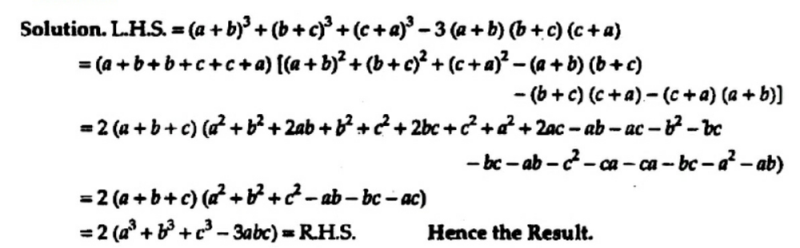
Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A3 B3 C3