Solved Prove The Following Theorem Rigorously Be Sure The Chegg

Solved Prove The Following Theorem Rigorously Be Sure The Chegg Prove that for any induced matrix norm ∥a∥ on mnxn(r), we have the consistency property: ∥ax∥≤∥a∥∥x∥ for all x∈rn. Math advanced math advanced math questions and answers carefully and rigorously prove the following. please do not skip any steps. (note this theorem comes from rudin's principles of mathematical analysis theorem 3.42 p70).

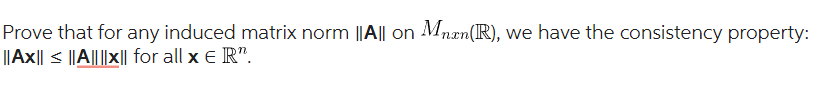
Solved Prove The Following Theorem Rigorously Be Sure The Chegg Question: prove the following rigorously (and justify the steps that you're writing): prove the following rigorously (and justify the steps that you're writing): you may use the quotient remainder theorem (qrt). Here’s the best way to solve it. prove rigorously each of the following statements using the definition of o, ohm, and theta. be sure to give values of c and n 0 that will make the argument work. a. (n^4 n^2 n 10 belongsto ohm (n^3) b. Theorem 157. the function f : r → r defined by for x e q, f (x) = for x e r\ q is continuous at a = 0 but not continuous at any other point in r. But what does it mean to prove rigorously that our approach cannot work? it can in fact mean various different things, but one way of demonstrating convincingly that an approach cannot work is to show that the same approach in a different context gives rise to a false result.

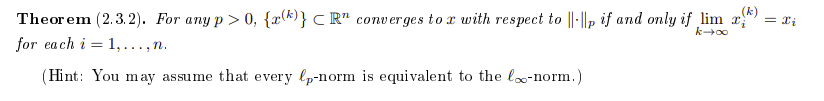
Prove The Following Theorem Rigorously Be Sure The Chegg Theorem 157. the function f : r → r defined by for x e q, f (x) = for x e r\ q is continuous at a = 0 but not continuous at any other point in r. But what does it mean to prove rigorously that our approach cannot work? it can in fact mean various different things, but one way of demonstrating convincingly that an approach cannot work is to show that the same approach in a different context gives rise to a false result. I'm trying to construct a rigorous proof for the divergence theorem, but i'm far from my goal. so far, i have constructed a basic proof, but it is filled with errors, assumptions, non rigorousness, etc. i want to make it rigorous; in so doing, i will learn how to construct rigorous proofs. Build a bridge using corollaries, axioms, and theorems to get to the declarative statement. take the quiz. what 8 concepts are covered in the proofs calculator?. A proof is a succession of "trivial" steps, leading from one statement to another. to be perfectly rigorous, the trivial steps should be either axioms, or theorems proven in equally rigorous manner (and references to said proofs). To prove the pythagorean theorem using similar triangles, let's start with a right triangle named abc, where angle c is the right angle. the lengths of the legs are labeled as 'a' (side ab) and 'b' (side ac), and the hypotenuse is labeled as 'c' (side bc).