Solved Q1 Solve The Following Problem Utt 4uxx 0

Solved Q1 Solve The Following Problem 0 0 U X 0 0 Ut X 0 X 0 Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. Since we're interested in the solution on 0 < x < 1, the method of reflection can be applied to solve the pde. consider the same problem over the whole line, where the odd extension of u(x; 0) is used in order to satisfy the dirichlet boundary condition at x = 0.

Solved Q1 Solve The Following Problem Utt 4uxx 0 To solve the problem utt 4uxx = 0 with the initial conditions u (x, 0) = sin (t) and ut (x, 0) = 1 (1 x²), we can use the method of separation of variables. Sign in to answer this question. solve the boundary value problem utt=4uxx learn more about boundary value problem. Given u(x,0) = 0 and ut(x,0) = x(4−x), we need to find u(xi,Δt). let’s denote Δt = k. the values of u(xi,tn) for i = 0,1,2,3,4 and n = 1,2,3,4 can be computed using the above steps. the final solution will be a table of values for each xi at each time step tn. For 0 < x < 5 and t > 0, find the solution to the following partial differential equation: ∂u ∂t = ∂²u ∂x², with the following boundary and initial conditions:.

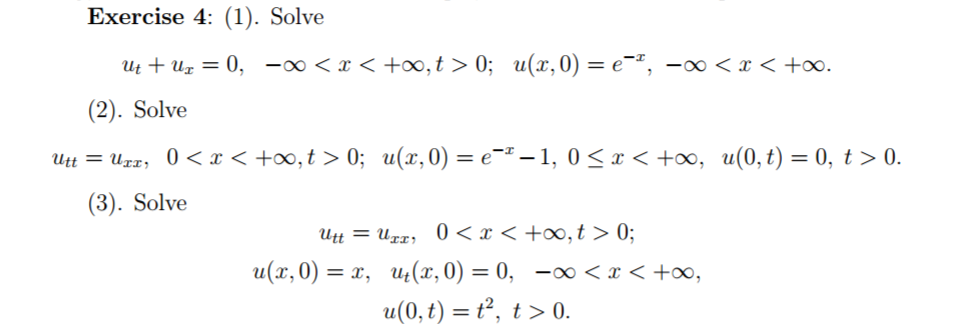
Solved Exercise 4 1 Solve 2 Solve Utt U 0 Given u(x,0) = 0 and ut(x,0) = x(4−x), we need to find u(xi,Δt). let’s denote Δt = k. the values of u(xi,tn) for i = 0,1,2,3,4 and n = 1,2,3,4 can be computed using the above steps. the final solution will be a table of values for each xi at each time step tn. For 0 < x < 5 and t > 0, find the solution to the following partial differential equation: ∂u ∂t = ∂²u ∂x², with the following boundary and initial conditions:. This question belongs to finding the solution of given differential equation . here we use d alembert principle to solve equation. any doubt can be clarify in comment section. thank you!!!. Since $d$ cannot be zero (otherwise the solution would be trivial), we must have $\sin (\frac {k} {2}) = 0$. this implies that $k = 2n\pi$ for some integer $n$. Applying the initial conditions u (x, 0) = x^2 – 2x and ut (x, 0) = 0, we can find the coefficients a n, c n, and d n by using the orthogonality property of sine functions. This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts.