Solved Quantifiers For All Universal Quantifier Chegg

Solved Quantifiers For All Universal Quantifier Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: quantifiers: (for all, universal quantifier), (there exists, existential quantifier). The phrase “for every” (or its equivalents) is called a universal quantifier. the phrase “there exists” (or its equivalents) is called an existential quantifier.

Solved Quantifiers For All Universal Quantifier Chegg Sentences that contain words like "all," "every," "each," "each and every," "any" (in some contexts), "everything," "anything," or any word that conveys the sense of "all" will be symbolized by using the universal quantifier. Video answers for all textbook questions of chapter 10, quantifiers – for all and there exists, how to think like a mathematician by numerade. Test your understanding of universal quantifiers with questions about alternative ways to express 'for all x, p (x)', the meaning of 'for any x, p (x)', different notations for the universal quantifier, and identifying statements that are universal quantifiers. We now have an elimination rule for the universal quantifier, and an introduction rule for the existential quantifier. this means that we can draw inferences from universally quantified sentences (∀ sentences), and to existentially quantified sentences (∃ sentences).
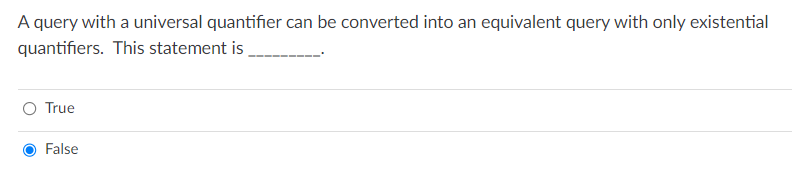
Solved A Query With A Universal Quantifier Can Be Converted Chegg Test your understanding of universal quantifiers with questions about alternative ways to express 'for all x, p (x)', the meaning of 'for any x, p (x)', different notations for the universal quantifier, and identifying statements that are universal quantifiers. We now have an elimination rule for the universal quantifier, and an introduction rule for the existential quantifier. this means that we can draw inferences from universally quantified sentences (∀ sentences), and to existentially quantified sentences (∃ sentences). There are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. answer to which of the following is a universal quantifier?. Definition: two statements involving predicates and quantifiers are logically equivalent iff they take on the same truth value regardless of which predicates are substituted into these statements and which domains of discourse are used. Example 5 let p(x) denote the statement “x > 3.” what is the truth value of the quantification x p(x), where the domain consists of all real numbers? solution: because “x > 3” is sometimes true—for instance, when x = 4—the existential quantification of p(x), which is x p(x), is true. Quantifiers are symbols or words used in logical statements to indicate the quantity of elements being referred to. they are essential in forming statements in mathematical logic and set theory. there are two types of quantifiers: the symbol ∀ means "for all" or "for every.".
Comments are closed.