Solved Question 1 Let A 1 2 3 4 5 6 And 4 2 5 6 6 1 2 Chegg

Solved 3 Let A 1 2 3 4 5 6 And 1 2 3 4 5 6 P1 Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: question 1. let a = {1,2,3,4,5,6} and: 4 2 5 6 6 1 2 3 4 2 3 1 5 and p3 = 2 3 3 2 1 2 3 p1 = 3 4 1 compute: a) pi! b) (p20 p1) p2; c) p10 (p3 0 pz'); d) p30 (p20pı) 1. question 2. Let's solve the question step by step. we start with the set a= {1,2,3,4,5,6}. the relation r is defined as: this means that for each element x in set a, y is the element that is one more than x. draw arrows from each element x in the domain to the corresponding y in the codomain based on the pairs we found.

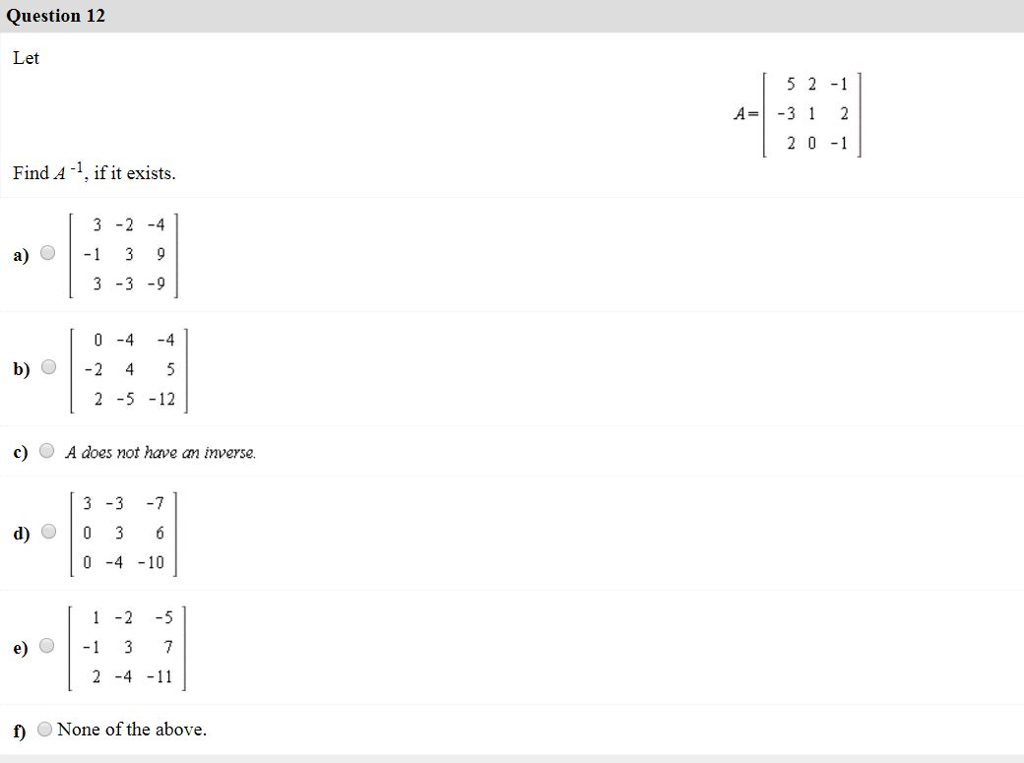
Solved Question 12 Let 5 2 1 4 1 31 2 0 1 Find A If It Chegg What is the order of each of the following permutations? (a) letαbe the permutation. thenα= (12) (356). α 2 = ( (12) (356)) 2 = (12) 2 (356) 2 = (365), α 3 = ( (12) (356)) 3 = (12) 3 (356) 3 = (12), α 4 = (356), α 5 = (12) (365), α 6 =e. thus|α|= 6. indeed, you may find a pattern. A∪b={1,2,3,4,5,6}. a. the union of two sets, denoted by a∪b, includes all unique elements from both sets a and b. in this case, set a is {1,2,3,4,5,6} and set b is {4,5,6}. the union of a and b, a∪b, will include all elements from both sets without repetition. therefore, the correct answer is: a. a\cup b=\ {1,2,3,4,5,6\}. a∪b={1,2,3,4,5. (iii) {5, 25, 125, 625} (iv) {2, 4, 6 upto infinity} (v) {1, 4, 9, upto 100} q: write the following sets in roster form: (i) a = {x: x is an integer and 3 < x < 7}. (ii) b = {x: x is a natural number less than 6}. (iii) c = {x: x is a two digit natural number such that the sum of its digits is 8} (iv) d = {x: x is a prime number which is. Show that the relation r in the set a = {1, 2, 3, 4, 5} given by r = { (a, b) |a − b| is even} is an equivalence relation. a company has four categories of employees given by assistants (a), clerks (c), managers (m), and an executive officer (e).

Solved Question 1 Let A 1 2 3 4 5 6 And 4 2 5 6 6 1 2 Chegg (iii) {5, 25, 125, 625} (iv) {2, 4, 6 upto infinity} (v) {1, 4, 9, upto 100} q: write the following sets in roster form: (i) a = {x: x is an integer and 3 < x < 7}. (ii) b = {x: x is a natural number less than 6}. (iii) c = {x: x is a two digit natural number such that the sum of its digits is 8} (iv) d = {x: x is a prime number which is. Show that the relation r in the set a = {1, 2, 3, 4, 5} given by r = { (a, b) |a − b| is even} is an equivalence relation. a company has four categories of employees given by assistants (a), clerks (c), managers (m), and an executive officer (e). To solve the given problem step by step, we will follow the instructions provided in the question. we are given a set a= {1,2,3,4,5,6} and a relation r defined by the rule r= {(x,y): y = x 1}. the arrow diagram visually represents the relation r. domain: the set of all first elements x in the pairs of r. here, the domain is:. Find step by step discrete maths solutions and the answer to the textbook question let a = {1, 2, 3, 4} and b = {1, 2, 3, 4, 5, 6}. (a) how many functions are there from a to b?. Let a = {1, 2, 3, 4, 5} and b = {1, 2, 3, 4, 5, 6}. then the number of functions f : a → b satisfying f (1) f (2) = f (4) – 1 is equal to. Since a = {a, b, c, d} has 4 elements and b = {1, 2, 3, 4, 5, 6} has 6 elements in it, the total number of one to one functions possible is: = (6 possibilities for mapping a) × (5 possibilities for mapping b) × (4 possibilities for mapping c) × (3 possibilities for mapping d) = 360.

Solved Let U 1 2 3 4 5 6 7 8 9 10 A 1 2 3 4 5 B Chegg To solve the given problem step by step, we will follow the instructions provided in the question. we are given a set a= {1,2,3,4,5,6} and a relation r defined by the rule r= {(x,y): y = x 1}. the arrow diagram visually represents the relation r. domain: the set of all first elements x in the pairs of r. here, the domain is:. Find step by step discrete maths solutions and the answer to the textbook question let a = {1, 2, 3, 4} and b = {1, 2, 3, 4, 5, 6}. (a) how many functions are there from a to b?. Let a = {1, 2, 3, 4, 5} and b = {1, 2, 3, 4, 5, 6}. then the number of functions f : a → b satisfying f (1) f (2) = f (4) – 1 is equal to. Since a = {a, b, c, d} has 4 elements and b = {1, 2, 3, 4, 5, 6} has 6 elements in it, the total number of one to one functions possible is: = (6 possibilities for mapping a) × (5 possibilities for mapping b) × (4 possibilities for mapping c) × (3 possibilities for mapping d) = 360.