
Solved Suppose We Have A Vector Space V And A Set Of Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. 5. s need not be a basis of v but will be a basis of linear span …. Problem 1. 5 (a), (b), (c) : let v be a vector space; let {a α} � of vectors of v , as α ranges over some index set j ( which may be infinite we say that the set { a α } spans v if every vector x in v can.

Solved Suppose We Have A Vector Space V And A Set Of Chegg Question: if s is a linearly independent set of vectors in vector space v, and s is not a basis for v, which of the following is true? s can be made into a basis for v by removing specific vectors from s. there exists a basis t for v, where t contains the same number of vectors as s. I am working from erwin kreyszig's book, where he mentions of a question. is the given set of vectors a vector space. if yes, determine the dimension and find a basis $(v {1},v {2},\cdots,v {n} )$ denote components. all vectors in $\mathbb r^{3}$, such that $4v {2} v {3}=k$. Determine whether the given set is a vector space. if not, give at least one axiom that is not satisfied. unless otherwise stated, assume that vector addition and scalar multiplication are the ordinary operations defined on the set. answer: this is not a vector space. If v is a vector space and s v is a subset which is closed under addition and scalar multiplication: then s is a vector space as well (called of course a subspace). problem 5.3. if s v be a linear subspace of a vector space show that the relation on v.

Solved 3 Suppose We Have A Vector Space V And A Set Of Chegg Determine whether the given set is a vector space. if not, give at least one axiom that is not satisfied. unless otherwise stated, assume that vector addition and scalar multiplication are the ordinary operations defined on the set. answer: this is not a vector space. If v is a vector space and s v is a subset which is closed under addition and scalar multiplication: then s is a vector space as well (called of course a subspace). problem 5.3. if s v be a linear subspace of a vector space show that the relation on v. A nonempty set v whose vectors (or elements) may be combined using the operations of addition ( ) and multiplication · by a scalar is called a vector space if the conditions in a and b below are satified: note an element or object of a vector space is called vector. Theorem 1: the span of any vectors in a subspace, v, is a subspace. prove it. suppose that a vector, w, in a vector space v has the property that u w=w u=u where u is any vector in v. in particular, 0 w=0 where 0 is the zero vector in v. but 0 w=w by axiom four. hence w=0 w=0 and we see that the zero vector is unique. redo problem 27 in 4.1. If you know how the operator and scalar multiplication have been defined, it's enough to check that the vector space is closed under the operators, ie. if you have any two vectors from your set, say u,v in v, and any scalar c, you have to verify that u v in v and cv in v. If a set s of vectors in a vector space v is linearly independent then , it is a basis of the linear span of s . it cannot contain more element than a set of vectors that spsn v . cannot contain the vector 0 .

Solved Question 18 A A Vector Space V Consists Of The Chegg A nonempty set v whose vectors (or elements) may be combined using the operations of addition ( ) and multiplication · by a scalar is called a vector space if the conditions in a and b below are satified: note an element or object of a vector space is called vector. Theorem 1: the span of any vectors in a subspace, v, is a subspace. prove it. suppose that a vector, w, in a vector space v has the property that u w=w u=u where u is any vector in v. in particular, 0 w=0 where 0 is the zero vector in v. but 0 w=w by axiom four. hence w=0 w=0 and we see that the zero vector is unique. redo problem 27 in 4.1. If you know how the operator and scalar multiplication have been defined, it's enough to check that the vector space is closed under the operators, ie. if you have any two vectors from your set, say u,v in v, and any scalar c, you have to verify that u v in v and cv in v. If a set s of vectors in a vector space v is linearly independent then , it is a basis of the linear span of s . it cannot contain more element than a set of vectors that spsn v . cannot contain the vector 0 .
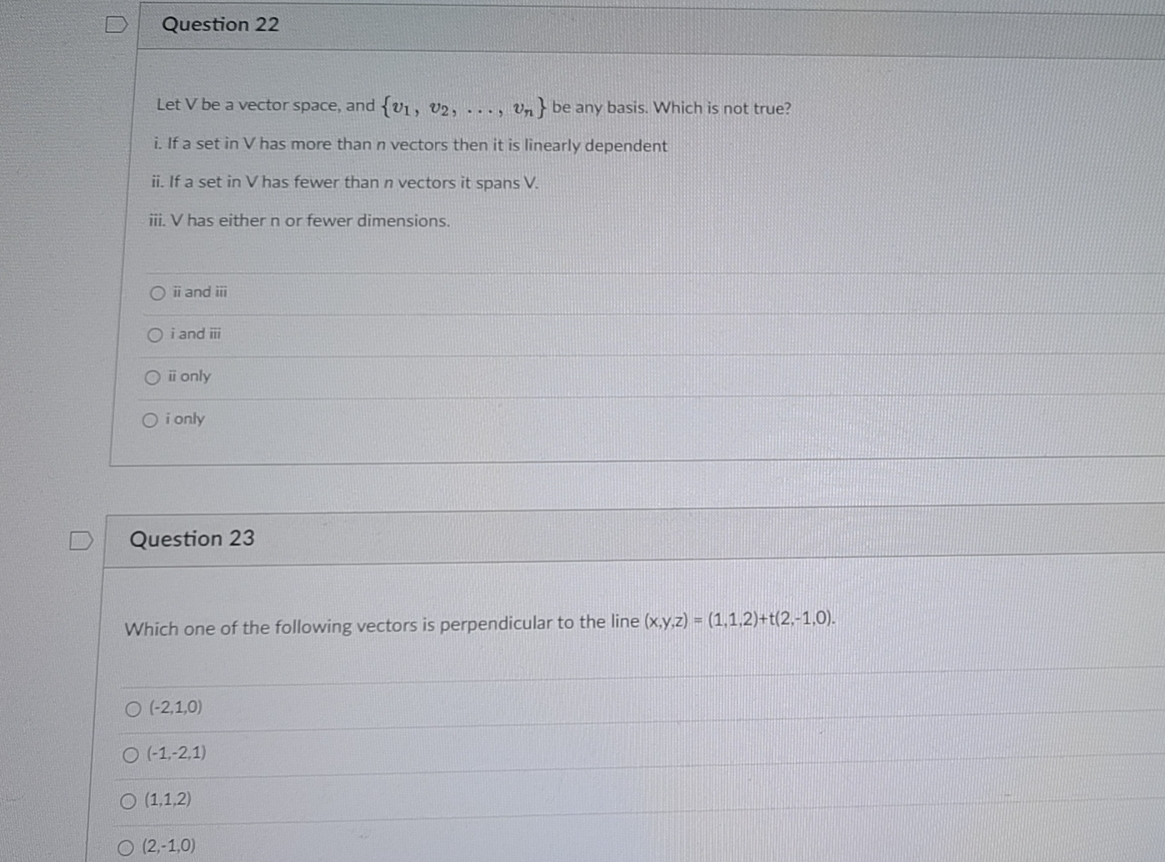
Solved U Question 22 Let V Be A Vector Space And V1 V2 Chegg If you know how the operator and scalar multiplication have been defined, it's enough to check that the vector space is closed under the operators, ie. if you have any two vectors from your set, say u,v in v, and any scalar c, you have to verify that u v in v and cv in v. If a set s of vectors in a vector space v is linearly independent then , it is a basis of the linear span of s . it cannot contain more element than a set of vectors that spsn v . cannot contain the vector 0 .
