
Solved Question 7 Let A Aa A11 A12 A21 A22 Where A11 Chegg Show that a can be factored into the product i 0 a11 a12 В І С where b = a21a11 and c = a22 – a21a11 a12. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Question: let a ∈ r n×n . partition it as a = a11 a12 a21 a22 , where a11 ∈ r k×k and a22 ∈ r (n−k)×(n−k) . the matrix a22 − a21a−1 11 a12 is called the schur complement of a, provided a11 is invertible. (a) prove that: if a is symmetric positive definite (spd), then its schur complement is spd too.

Solved Question 5 Let A11 A12 At At A And At A21 A22 Az Chegg Step 1 determine every minor for the 2x2 matrix. matrix a = a11 a12 a21 a22. determine the minor for each element. this is done by selecting an element, amn, where m is the row and n the column. eliminate from the matrix the rows m and columns n as in the selected element. To show that the inverse of matrix a a is as given, we need to verify that a \cdot a^ { 1} = i a⋅ a−1 = i, where i i is the identity matrix. we will compute the product of a a and the given a^ { 1} a−1 and check if it results in the identity matrix. To prove the given formula for the inverse of a partitioned matrix, we will use block matrix multiplication and properties of block matrices. here's the step by step proof: given matrix ?=(?11?12?21?22)a=(a11?a21??a12?a22??) and the partitioned matrices. Use these matrices to show that each statement is true for 2×2 matrices.let a=[a11 a21 a12 a22],b=[b11 b21 b12 b22], and c =[c11 c21 c12 c22] where all the elements are real numbers. a(b c)=ab ac (distributive property) a sample has a mean of m =90 and a standard deviation of s = 20 a.
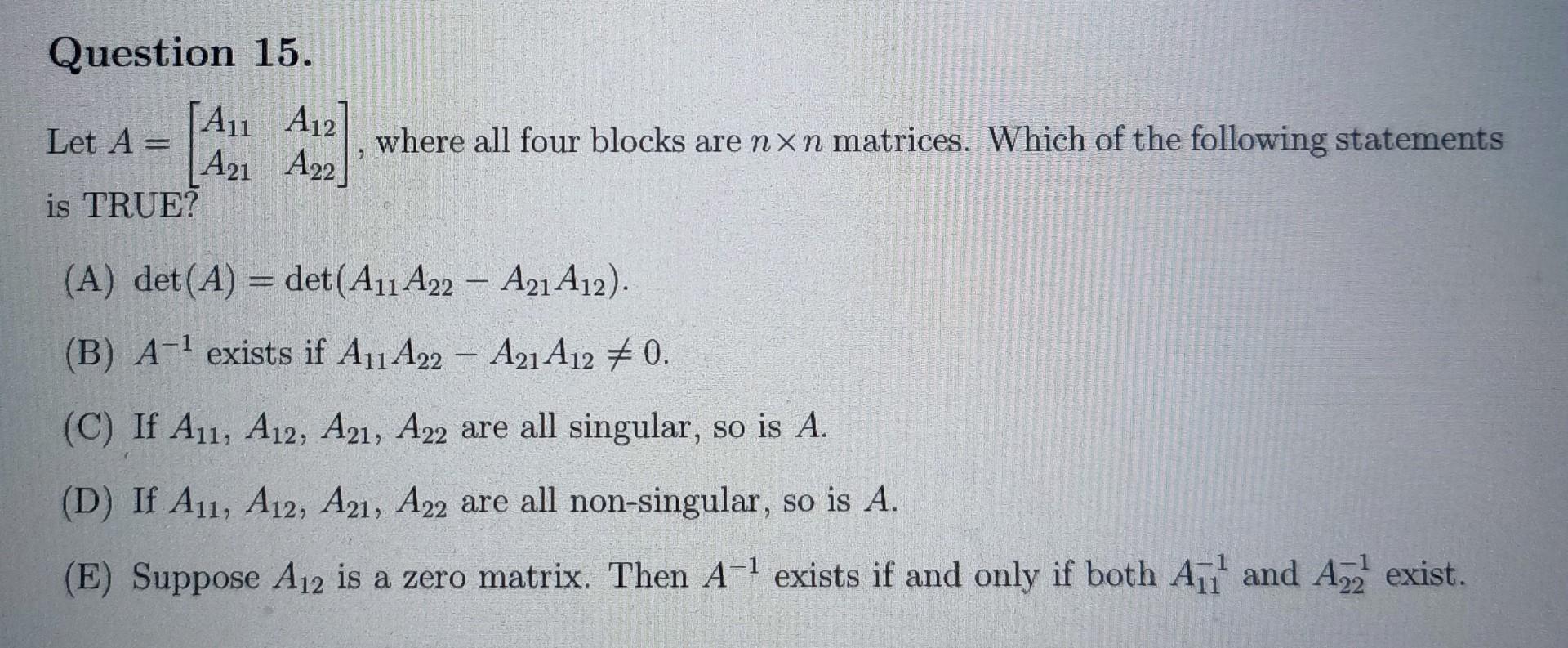
Question 15 A1 A12 Let A A21 A22 Is True Where Chegg To prove the given formula for the inverse of a partitioned matrix, we will use block matrix multiplication and properties of block matrices. here's the step by step proof: given matrix ?=(?11?12?21?22)a=(a11?a21??a12?a22??) and the partitioned matrices. Use these matrices to show that each statement is true for 2×2 matrices.let a=[a11 a21 a12 a22],b=[b11 b21 b12 b22], and c =[c11 c21 c12 c22] where all the elements are real numbers. a(b c)=ab ac (distributive property) a sample has a mean of m =90 and a standard deviation of s = 20 a. Let a=[a11, a12, a21, a22]show that if d=a11a22 a21a12 = 0, thena^ 1 = (1 d)[a22, a12, a21, a11] your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Solution for consider the equation a = [a11 a12; a21 a22] where t = tt. also, let a = [2 1; 2 2], a21 = 1, and a22 = 0. take a11 = 0, a12 = 1. the origin in state space is an equilibrium. Showing that a function is an inner product let a=[a11 a12 a21 a22]and b=[b11 b12 b21 b22]be matrices in the vector space m 2,2 . show that the function defines an inner product on m 2,2 . this textbook is available at. Let \[ a=\left(\begin{array}{ll} a {11} & a {12} \\ a {21} & a {22} \end{array}\right) \] show that if $d=a {11} a {22} a {21} a {12} \neq 0$, then \[ a^{ 1}=\frac{1}{d}\left(\begin{array}{rr} a {22} & a {12} \\ a {21} & a {11} \end{array}\right) \] 13.

Solved 1 Point Let B 7 7 Then A11 A12 Ab A21 A22 Where Chegg Let a=[a11, a12, a21, a22]show that if d=a11a22 a21a12 = 0, thena^ 1 = (1 d)[a22, a12, a21, a11] your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Solution for consider the equation a = [a11 a12; a21 a22] where t = tt. also, let a = [2 1; 2 2], a21 = 1, and a22 = 0. take a11 = 0, a12 = 1. the origin in state space is an equilibrium. Showing that a function is an inner product let a=[a11 a12 a21 a22]and b=[b11 b12 b21 b22]be matrices in the vector space m 2,2 . show that the function defines an inner product on m 2,2 . this textbook is available at. Let \[ a=\left(\begin{array}{ll} a {11} & a {12} \\ a {21} & a {22} \end{array}\right) \] show that if $d=a {11} a {22} a {21} a {12} \neq 0$, then \[ a^{ 1}=\frac{1}{d}\left(\begin{array}{rr} a {22} & a {12} \\ a {21} & a {11} \end{array}\right) \] 13.
