Solved Show That A B 2 Is Different From A 2 2ab Chegg
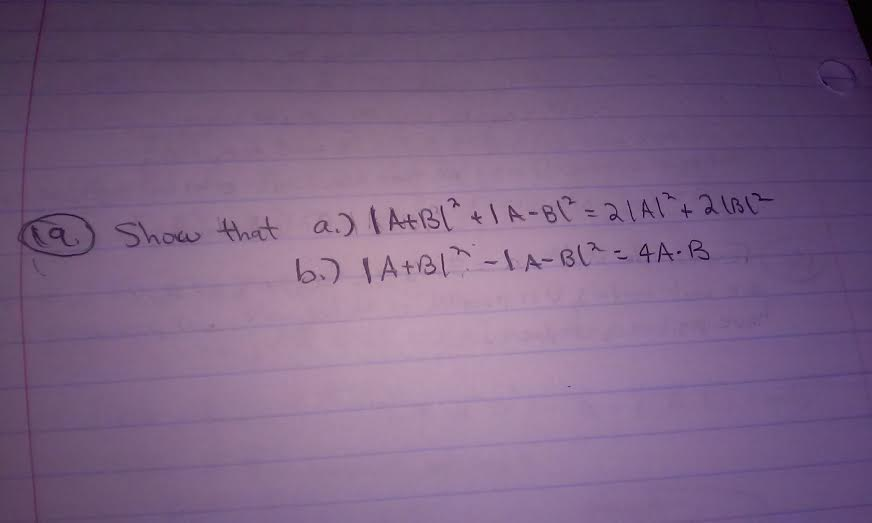
Solved Show That A B 2 A B 2 2 A 2 2 B 2 Chegg Facebook will not allow developers pre fill messages. developers may customize the story by providing og meta tags, but it's up to the user to fill the message. this is only possible if you are posting on the user's behalf, which requires the user authorizing your application with the publish actions permission. and even then:. Facebook downloads the audio and the video separately, so get the audio link from the google chrome inspector, by right click on the video and choosing inspect ,going to inspector, network tab, and checking the links, use filter:larger than:50k in the filter area to select bigger files (change 50k according to the length of your video), look in.
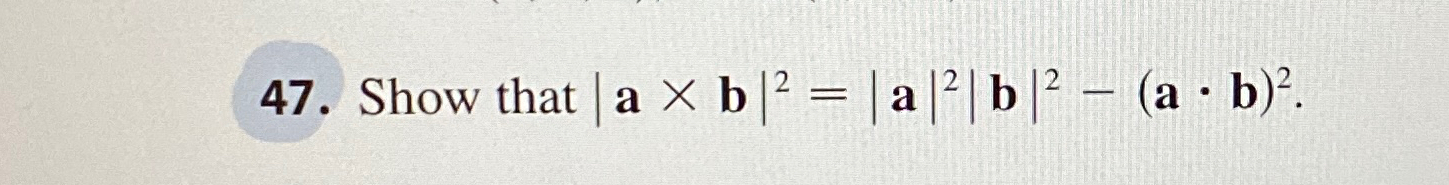
Solved Show That A B 2 A 2 B 2 A B 2 Chegg In the facebook developers console for your app, go to app review > permissions and features. set the public profile and email to have advanced access. this will allow all facebook users to have access and these two settings are auto granted. ensure the access level indicates advanced access. It doesn't work,browser do not allow to load local files to iframe, if you try to load an html from the server you get "refused to display ' m.facebook ' in a frame because it set 'x frame options' to 'deny'.". This is in fact the correct answer, was able to extract link with chrome developer tools through m.facebook. I have written a code to record audio and save it to below file location. private string getfilename() { string filepath = environment.getexternalstoragedirectory().getpath(); file file =.

Solved Show That A B 2 Is Different From A 2 2ab Chegg This is in fact the correct answer, was able to extract link with chrome developer tools through m.facebook. I have written a code to record audio and save it to below file location. private string getfilename() { string filepath = environment.getexternalstoragedirectory().getpath(); file file =. Facebook obtain location places id via location name asked 14 years, 5 months ago modified 7 years, 5 months ago viewed 24k times. Important notice: if you register for testing, go to your profile settings and to your interests add delete profile. trying to login with facebook to my website: i get the following error: url. If i use the like button instead of facebook sharer. how can i change the content of the share option?. Sso today suddenly i had two unauthorized automatic payments to meta platforms inc (email says facebook ireland???) amounting to $354.72! i checked my facebook account and there were no activities logged. it's no small sum and when i raised a dispute to paypal, paypal denied the dispute and deeme.

Solved Show That A B 2 Is Different From A 2 2ab Chegg Facebook obtain location places id via location name asked 14 years, 5 months ago modified 7 years, 5 months ago viewed 24k times. Important notice: if you register for testing, go to your profile settings and to your interests add delete profile. trying to login with facebook to my website: i get the following error: url. If i use the like button instead of facebook sharer. how can i change the content of the share option?. Sso today suddenly i had two unauthorized automatic payments to meta platforms inc (email says facebook ireland???) amounting to $354.72! i checked my facebook account and there were no activities logged. it's no small sum and when i raised a dispute to paypal, paypal denied the dispute and deeme.
Comments are closed.