
Solved Solutions In Particular Solve The Ivps In Problem Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: solutions in particular solve the ivps in problems 13 16. 13. x′= [11−11]x,x (0)= [−11]x′= [11−5−3]x,x (0)= [54] there are 2 steps to solve this one. find the eigenvalues of the coefficient matrix. the characterist. Solutions in particular solve the ivps in problems 25 34. sketch the trajectory. x ′ = [− 2 − 5 1 4 ] x, x (0) = [1 3 ].
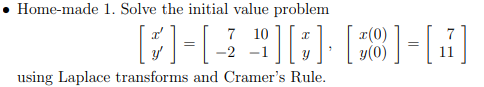
Solved Solutions In Particular Solve The Ivps In Problem Chegg Solution: first, we know f (t; y) = 1 t sin(ty) is continuous on [0; 2] r. second, we can see. so f (t; y) is lipschitz with respect to y (with constant 4). from theorem above, we know the ivp has a unique solution y(t) on [0; 2]. f by (t) and initial value y(a) by change to original solution y(t). let d = [a; b] r. You will learn how taylor series can be used to solve some initial value problems. we begin this method of solving initial value problems by assuming that the solution can be written as a taylor series expanded about 0. we substitute a “generic” series into the differential equation and then determine what its coefficients must be. Solving initial value problems (ivps) is an important concept in differential equations. like the unique key that opens a specific door, an initial condition can unlock a unique solution to a differential equation. as we dive into this article, we aim to unravel the mysterious process of solving initial value problems in differential equations. Examples of solving ivp’s . example 1. solve x 3x = e t with rest initial conditions (rest ic). . solution. rest ic mean that x(t) = 0 for t < 0, so x(0 ), x(0 ), . . . are all 0. as usual, we let x = l(x). using the t derivative rule we can take the laplace transform of (both sides) of the de. (sx(s) x(0 )) 3x(s) = 1 (s 1).

Solved Solutions In Particular Solve The Ivps In Problems Chegg Solving initial value problems (ivps) is an important concept in differential equations. like the unique key that opens a specific door, an initial condition can unlock a unique solution to a differential equation. as we dive into this article, we aim to unravel the mysterious process of solving initial value problems in differential equations. Examples of solving ivp’s . example 1. solve x 3x = e t with rest initial conditions (rest ic). . solution. rest ic mean that x(t) = 0 for t < 0, so x(0 ), x(0 ), . . . are all 0. as usual, we let x = l(x). using the t derivative rule we can take the laplace transform of (both sides) of the de. (sx(s) x(0 )) 3x(s) = 1 (s 1). Video answer: solutions in particular solve the ivps in problems 25 34. sketch the trajectory. \overrightarrow{\mathbf{x}}^{\prime}=\left[\begin{array}{ll}1 & 1 \\ 1 & 1\end{array}\right] \overrightarrow{\mathbf{x}. Solve the initial value problem [f] [3 ** ] [6] [es] [1] using laplace transforms and cramer's rule. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. In this section we will examine how to use laplace transforms to solve ivp’s. the examples in this section are restricted to differential equations that could be solved without using laplace transform. This problem has been solved: solutions for chapter 3.r problem 67p: find the solution of the ivps given in. … get solutions get solutions get solutions done loading looking for the textbook?.
