
Solved Solve Ax Vector B Vector Where A 3 4 2 3 B Chegg Solve the ax=b equation and find the x vector using gauss elimination algorithm. write all the steps of the matrix operations with your handwriting given a and b below. a=⎣⎡8−20−24−30−33⎦⎤,b=⎩⎨⎧2−13⎭⎬⎫. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. In this section we will learn how to solve the general matrix equation ax = b for x. we will start by considering the best case scenario when solving a→x = →b; that is, when a is square and we have exactly one solution. for instance, suppose we want to solve a→x = →b where. a = [1 1 2 1] and →b = [0 1].

Solved Find A And B That Solve The Vector Equation Chegg We have been going through how to solve the system of equations known as $ax=b$, where $a$ is a matrix, $x$ is a vector and $b$ is a vector. i understand that if we have $a$ and $b$ we must find out what $x$ is, this happens via gauss jordan elimination, back substitution, etc. One way to find a particular solution to the equation ax = b is to set all free variables to zero, then solve for the pivot variables. which has the solution x3 = 3 2, x1 = −2. our particular solution is: the general solution to ax = b is given by xcomplete = xp xn, where xn is a generic vector in the nullspace. To solve the equation ax = b, find the inverse of matrix a and multiply it with b to find vector x. the steps involve ensuring a is invertible, calculating its inverse, and performing the multiplication. Consider solving the equation ax=b where x is an unknown vector, b is a known vector and the matrix a is given by a=⎣⎡430011132⎦⎤. if the vector b is accurate only to 10−5, how accurate will be the solution x in terms of 1 norm? your solution’s ready to go!.
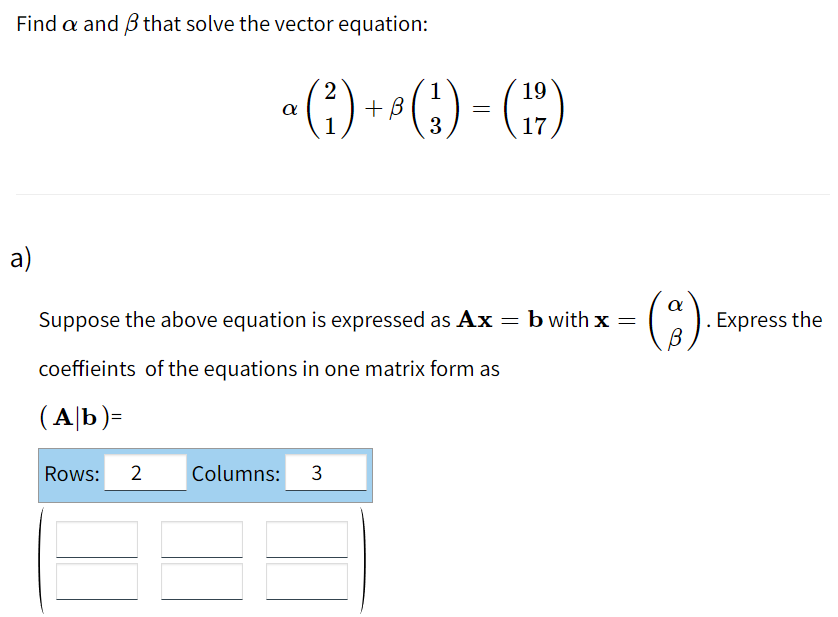
Solved Find A And B That Solve The Vector Equation 2 α A Chegg To solve the equation ax = b, find the inverse of matrix a and multiply it with b to find vector x. the steps involve ensuring a is invertible, calculating its inverse, and performing the multiplication. Consider solving the equation ax=b where x is an unknown vector, b is a known vector and the matrix a is given by a=⎣⎡430011132⎦⎤. if the vector b is accurate only to 10−5, how accurate will be the solution x in terms of 1 norm? your solution’s ready to go!. Free online vector calculator solve vector operations and functions step by step. This section is about solving the \matrix equation" ax = b, where a is an m n matrix and b is a column vector with m entries (both given in the question), and x is an unknown column vector with n entries (which we are trying to solve for). We know how to find the null space of a matrix as the full set of vectors x that satisfy ax=o. but now we want to be able to solve the more general equation ax=b. in other words, we want to be able to solve this equation when that vector on the right side is some non zero b, instead of being limited to solving the equation only when b=o. Solving ax=0 and ax=b null spaces definition 1. the null space of a matrix a is nul(a)={x : ax=0}. in other words, if a is m× n, then its null space consists of those vectors x∈ rn which solve the homogeneous equation ax=0. theorem 2. if a is m× n, then nul(a) is a subspace of rn. proof.

Solved Find A And B That Solve The Vector Equation 2 α A Chegg Free online vector calculator solve vector operations and functions step by step. This section is about solving the \matrix equation" ax = b, where a is an m n matrix and b is a column vector with m entries (both given in the question), and x is an unknown column vector with n entries (which we are trying to solve for). We know how to find the null space of a matrix as the full set of vectors x that satisfy ax=o. but now we want to be able to solve the more general equation ax=b. in other words, we want to be able to solve this equation when that vector on the right side is some non zero b, instead of being limited to solving the equation only when b=o. Solving ax=0 and ax=b null spaces definition 1. the null space of a matrix a is nul(a)={x : ax=0}. in other words, if a is m× n, then its null space consists of those vectors x∈ rn which solve the homogeneous equation ax=0. theorem 2. if a is m× n, then nul(a) is a subspace of rn. proof.
