Solved Solve The Following Ordinary Differential Equation In Terms Of

Solved Ordinary Differential Equationsolve The Following Chegg How do you calculate ordinary differential equations? to solve ordinary differential equations (odes), use methods such as separation of variables, linear equations, exact equations, homogeneous equations, or numerical methods. Calculator of ordinary differential equations. with convenient input and step by step!.

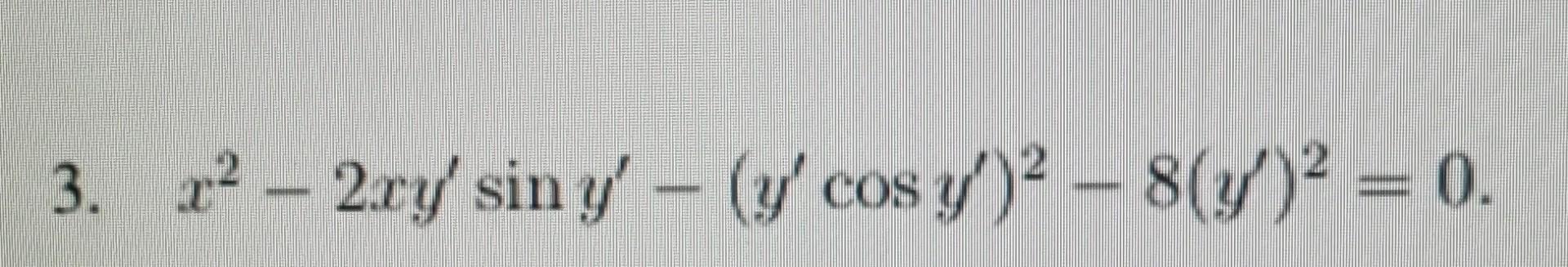
Solved Solve The Ordinary Differential Equation Solve Chegg Get the free "step by step differential equation solver" widget for your website, blog, wordpress, blogger, or igoogle. find more mathematics widgets in wolfram|alpha. In another lesson, we discuss how euler’s method is used to solve higher order and coupled (simultaneous) ordinary differential equations. how does one write a first order differential equation in the above form?. Free ordinary differential equations (ode) calculator solve ordinary differential equations (ode) step by step. Simple examples of solving ordinary differential equation.

Solved Ordinary Differential Equation Solve This Differential Free ordinary differential equations (ode) calculator solve ordinary differential equations (ode) step by step. Simple examples of solving ordinary differential equation. The following table introduces the types of equations that can be solved by dsolve. examples of odes belonging to each of these types are given in other tutorials (clicking a link in the table will bring up the relevant examples). A function y = y(x) is a solution of an ordinary differential equation on an open interval if the equation is satisfied identically on the interval when y and its derivatives are substituted into the equation. These notes introduce the analytical solution of ordinary differential equations. emphasis is placed on simple equations of first and second order, with emphasis on equations with constant coefficients. brief treatment is given to nonhomogeneous equations of second and higher orders. The first order differential equation and the given initial value constitute a first order initial value problem given as: = ( , ) ; 0 = 0, whose numerical solution may be given using any of the following methodologies:.