
Solved Spherical Shell Charge Consider A Spherical Shell Chegg Consider a spherical shell with inner radius b, outer radius a, and total charge 2q uniformly distributed on the shell. you are going to calculate the electric field inside the shell using a gaussian sphere (gs) of radius r. a. how much charge is enclosed by gs? b. what is the total electric flux on gs? use the general definition of. When considering how to calculate the electric field of a charged spherical shell you first need to identify where the observation location is, and then follow the guidelines below. observation location outside of the spherical shell: [math]\displaystyle{ \vec{e} {sphere}=\frac{1}{4\pi e 0}\frac{q}{r^2}\widehat{r} }[ math].

Solved C Consider A Thin Spherical Shell Of Charge Chegg A thick spherical shell carries charge density ρ= k r2 (a≤r≤b) (fig. 2.25). find the electric field in the following three regions: (i) r
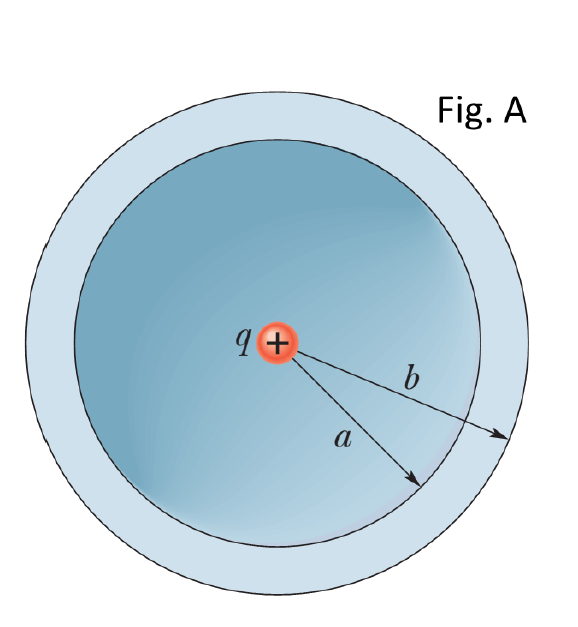
Solved Consider The Spherical Shell And Point Charge Q Chegg (a) calculate the electrostatic energy of the shell. we can term this energy as self energy of the shell. (b) calculate the work done in assembling a spherical shell of uniform charge q and radius r by bringing charges in small installments from infinity and putting them on the shell. do you find the answers in (a) and (b) to be same?. Problem: consider a spherical system with a central point charge of charge q and a thin spherical shell of charge with radius a and charge 2q. the region inside the shell is filled with a dielectric of constant k = 2. draw and compute the field everywhere. Today, i want to talk about the thin, charged spherical shell and show that one can use coulomb’s law rather than the traditional method of gauss’s law to solve it. suppose i have a charged spherical shell with radius \(r\) and total charge q. Consider two concentric spherical shells of radii $a$ and $2a$ respectively. let the inner shell have potential $v 0$ and the outer shell be grounded. what is the potential $v(r)$ as a function of the distance to the center of the shells, and what are the charges on the shells?. Consider a positive point charge q located at the center of a sphere of radius r, as shown in figure 4.2.1. the electric field due to the charge q is 2 0 e=( q4πεr)rˆ ur, which points in the radial direction. we enclose the charge by an imaginary sphere of radius r called the “gaussian surface.” 4 3. A spherical shell with inner radius a and outer radius b is uniformly charged with a charge density ρ. 1) find the electric field intensity at a distance z from the centre of the shell. 2) determine also the potential in the distance z.

Solved Question 5 Consider A Spherical Shell Formed From Chegg Today, i want to talk about the thin, charged spherical shell and show that one can use coulomb’s law rather than the traditional method of gauss’s law to solve it. suppose i have a charged spherical shell with radius \(r\) and total charge q. Consider two concentric spherical shells of radii $a$ and $2a$ respectively. let the inner shell have potential $v 0$ and the outer shell be grounded. what is the potential $v(r)$ as a function of the distance to the center of the shells, and what are the charges on the shells?. Consider a positive point charge q located at the center of a sphere of radius r, as shown in figure 4.2.1. the electric field due to the charge q is 2 0 e=( q4πεr)rˆ ur, which points in the radial direction. we enclose the charge by an imaginary sphere of radius r called the “gaussian surface.” 4 3. A spherical shell with inner radius a and outer radius b is uniformly charged with a charge density ρ. 1) find the electric field intensity at a distance z from the centre of the shell. 2) determine also the potential in the distance z.
