
Solved Test Each Of The Following Series For Convergence By Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test canbe applied to the series, enter conv if it converges or div if it diverges. For each of the following, say whether it converges or diverges and explain why. 1. p ∞ n=1 n3 5 3 answer: notice that n3 n5 3 < n3 n5 = 1 n2 for all n. therefore, since p 1 n2 converges (it’s a p series with p = 2 > 1), the series p n3 n5 3 also converges by the comparison test. 2. p ∞ n=1 3n 4n 4 answer: notice that 3 n 4n 4 < 3 4n.
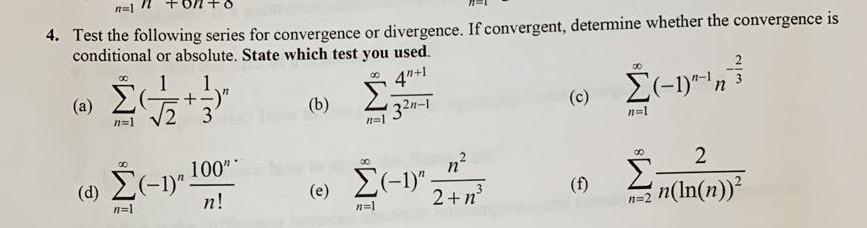
Solved 4 Test The Following Series For Convergence Or Chegg For each of the following series, determine which convergence test is the best to use and explain why. then determine if the series converges or diverges. if the series is an alternating series, determine whether it converges absolutely, converges conditionally, or diverges. ∞ ∑ n=1 (−1)n 1(3n 1) n! ∑ n = 1 ∞ (− 1) n 1 (3 n 1) n!. Here we show how to use the convergence or divergence of these series to prove convergence or divergence for other series, using a method called the comparison test. for example, consider the series \[\sum {n=1}^∞\dfrac{1}{n^2 1}.\]. Test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test can be applied to the series, enter conv if the series converges or div if it diverges. if neither test can be applied to the series, enter na. Test each of the following series for convergence, stating whether it converges or diverges, and justifying your answer by citing an appropriate convergence test and showing clearly how it applies. if there are limits involved, make sure to compute their precise values.

Solved Test The Convergence Of The Following Series A Chegg Test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test can be applied to the series, enter conv if the series converges or div if it diverges. if neither test can be applied to the series, enter na. Test each of the following series for convergence, stating whether it converges or diverges, and justifying your answer by citing an appropriate convergence test and showing clearly how it applies. if there are limits involved, make sure to compute their precise values. Determine if the series \( \displaystyle \sum\limits {n = 0}^\infty {{a n}} \) is convergent or divergent. if the series is convergent determine the value of the series. \(\displaystyle {s n} = \frac{{5 8{n^2}}}{{2 7{n^2}}}\) solution. Our expert help has broken down your problem into an easy to learn solution you can count on. question: (1 point) test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test can be appliedto the series, enter conv if it converges or div if it diverges. 7b 1 using the integral test, tell whether the following series converge or diverge; show work or reasoning. (in the last two, the answer depends on the value of the parameter p.) 7b 2 using the limit comparison test, tell whether each series converges or diverges; show work or reasoning. (for some of them, simple comparison works.). We have ve tests for convergence: 1) the divergence test, 2) the alternating series test, 3) the ratio test, 4) the integral (comparison) test, and 5) the comparison test. given.
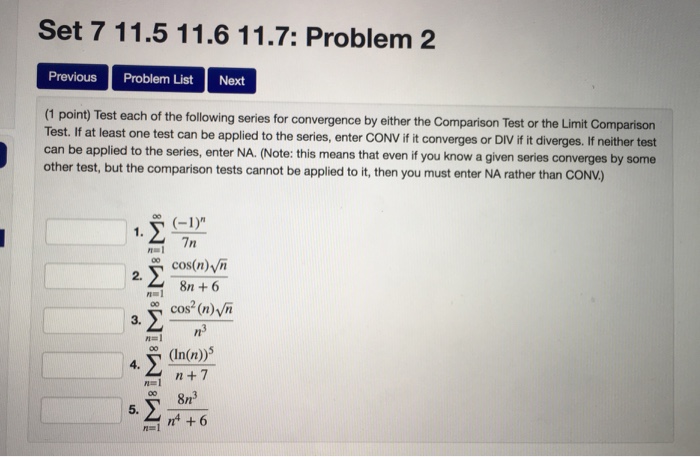
Solved Test Each Of The Following Series For Convergence By Chegg Determine if the series \( \displaystyle \sum\limits {n = 0}^\infty {{a n}} \) is convergent or divergent. if the series is convergent determine the value of the series. \(\displaystyle {s n} = \frac{{5 8{n^2}}}{{2 7{n^2}}}\) solution. Our expert help has broken down your problem into an easy to learn solution you can count on. question: (1 point) test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test can be appliedto the series, enter conv if it converges or div if it diverges. 7b 1 using the integral test, tell whether the following series converge or diverge; show work or reasoning. (in the last two, the answer depends on the value of the parameter p.) 7b 2 using the limit comparison test, tell whether each series converges or diverges; show work or reasoning. (for some of them, simple comparison works.). We have ve tests for convergence: 1) the divergence test, 2) the alternating series test, 3) the ratio test, 4) the integral (comparison) test, and 5) the comparison test. given.
