Solved The Two Sided Power Spectral Density Of Thermal Noise Chegg

Solved The Two Sided Power Spectral Density Of Thermal Noise Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: the two sided power spectral density of thermal noise which is modeled as additive white gaussian noise, is given by n 2=4,0e−5 w hz. Find the autocorrelations of the following ct and dt energy and power signals and show that, at zero shift, the value of the autocorrelation is the signal energy or power and that all the properties of autocorrelation functions are satisfied.

Solved The Two Sided Power Spectral Density Of White Noise Chegg Why study power spectral density? what is the usage of power spectral density? useful when we pass a random process through some linear operations. for example, convolution: running average, or running diference. fourier transform is useful to speed up the computation, and help drawing samples. Find the autocorrelation function of { x ( t ) }. (b) find at the first null in the autocorrelation function. (c) find the correlation between samples if this process is sampled at a rate of 250 hz. Two sided power spectral density of thermal noise at the photo detector can be expressed as 2kbt rl, where kb is the boltzmann constant. The data ak ̨ {–1} consists of independent identically distributed binary symbols, ht(t) is the transmit filter, hr(t) is the receiver filter, c(t) is the channel impulse response, and n(t) is awgn with the double sided power spectral density n0 2.
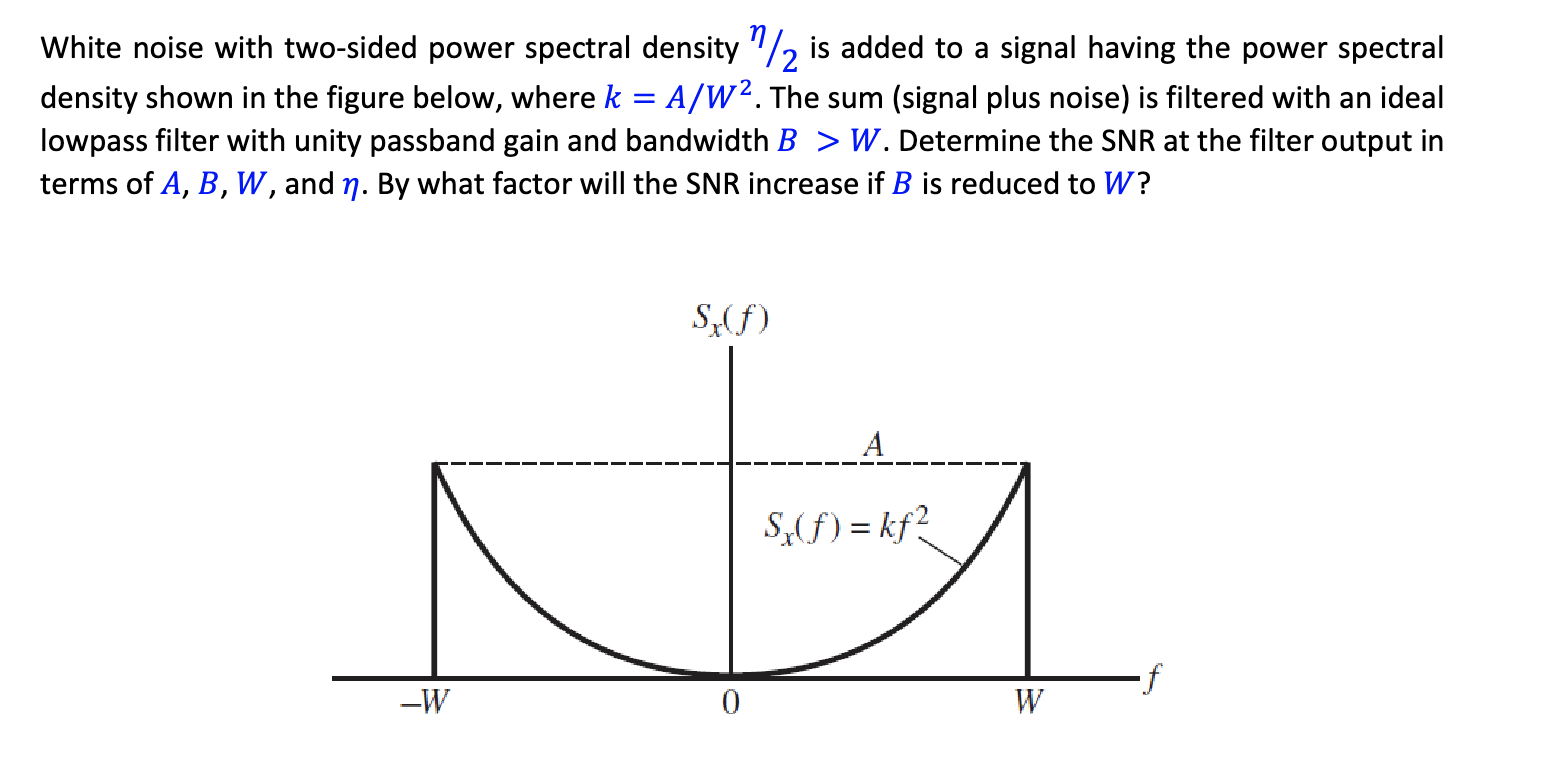
Solved White Noise With Two Sided Power Spectral Density η 2 Chegg Two sided power spectral density of thermal noise at the photo detector can be expressed as 2kbt rl, where kb is the boltzmann constant. The data ak ̨ {–1} consists of independent identically distributed binary symbols, ht(t) is the transmit filter, hr(t) is the receiver filter, c(t) is the channel impulse response, and n(t) is awgn with the double sided power spectral density n0 2. Let’s delve into the expression for the two sided power spectral density (psd) of thermal not the question you’re looking for? post any question and get expert help quickly. Built for deeper learning you get so much more than just the answer—you learn how to solve the problem and test your understanding. Since the noise is "white" it will be uniformly distributed across that given bandwidth and thus is the noise density in watts hz. at room temperature (300°k) this is approximately 174 dbm hz as a power spectral density. Bandlimited white noise is simply the response of an ideal lowpass filter that is excited by white noise. the psd of bandlimited white noise is constant over a finite frequency range and zero outside that range. bandlimited white noise has finite signal power.

The Power Spectral Density Psd Of The Thermal Noise Chegg Let’s delve into the expression for the two sided power spectral density (psd) of thermal not the question you’re looking for? post any question and get expert help quickly. Built for deeper learning you get so much more than just the answer—you learn how to solve the problem and test your understanding. Since the noise is "white" it will be uniformly distributed across that given bandwidth and thus is the noise density in watts hz. at room temperature (300°k) this is approximately 174 dbm hz as a power spectral density. Bandlimited white noise is simply the response of an ideal lowpass filter that is excited by white noise. the psd of bandlimited white noise is constant over a finite frequency range and zero outside that range. bandlimited white noise has finite signal power.
Solved White Noise With A Two Sided Power Spectral Density Chegg Since the noise is "white" it will be uniformly distributed across that given bandwidth and thus is the noise density in watts hz. at room temperature (300°k) this is approximately 174 dbm hz as a power spectral density. Bandlimited white noise is simply the response of an ideal lowpass filter that is excited by white noise. the psd of bandlimited white noise is constant over a finite frequency range and zero outside that range. bandlimited white noise has finite signal power.
Comments are closed.